Korešpondenčné kolo programátorskej súťaže ACM na FEI STU 20015.3.2001 - 8.4.2001
Problém A: Súkolie(sukolie.c | .C | .p) Inžinierska firma vyrábajúca súkolia potrebuje kontrolovať, či nimi navrhnutá sústava ozubených kolies bude pracovať podľa ich požiadaviek. Kontrolu návrhov chcú vykonávať bez toho, aby súkolia museli vyrobiť. Súkolia sú vždy navrhnuté pre špeciálnu montážnu plochu s úchytkami pre ozubené kolesá. Každé koleso má zuby v dvoch úrovniach (nad sebou), preto hovoríme o vnútornom (bližšie k montážnej ploche) a o vonkajšom (ďalej od montážnej plochy) polomere kolesa. Kolesá rotujú okolo svojho stredu a otáčajú tie kolesá v súkolí, ktorých sa dotýkajú (vo vnútornej alebo vo vonkajšej úrovni), rovnakou tangenciálnou rýchlosťou. Každé koleso sa otáča samozrejme rovnakou uhlovou rýchlosťou na oboch úrovniach. Špeciálna montážna plocha pre súkolia má na povrchu sieť 300x300 úchytných bodov. Ľavý dolný roh plochy má pozíciu x=1, y=1 a pravý horný roh má pozíciu x=300, y=300. Kolesá sa na plochu uchytávajú len v úchytných bodoch. Veľkosť vnútorného a vonkajšieho polomeru kolies je celé číslo z intervalu <1, 100>. Energia na otáčanie súkolia sa dodáva zo zadnej strany montážnej plochy a otáča práve jedným kolesom nazvaným „hnacie koleso“. Na obrázku je znázornené 1. súkolie z ukážkového príkladu:  Z týchto údajov je možné vypočítať, že koleso č.1 sa otáča v smere hodinových ručičiek (tento smer budeme označovať písmenom “S“) rýchlosťou 83.33 otáčok za minútu; koleso č.2 v protismere hodinových ručičiek rýchlosťou 187.50 (“P“); koleso č.3 v protismere hodinových ručičiek rýchlosťou 150.00 (“P“); koleso č.4 rotuje v smere hodinových ručičiek rýchlosťou 281.25 (“S“) a koleso č.5 v protismere hodinových ručičiek 33.75 (“P“). Napriek tomu, že v tomto príklade sa nevyskytujú žiadne poruchy, firma potrebuje program, ktorý označí dva typy porúch, ktoré sa v ich návrhoch občas vyskytnú. Prvá porucha nastáva vtedy, keď sa dve, alebo viac kolies prekrývajú na vnútornej alebo na vonkajšej úrovni. Druhá porucha nastane v situácii, ak by malo byť niektoré z kolies súčasne otáčané viacerými kolesami rôznymi rýchlosťami. Je však povolené, aby bolo koleso otáčané aj viacerými kolesami za podmienky, ak je všetkými týmito kolesami otáčané v jednom smere rovnakou rýchlosťou. Situácia, ktorá ešte nie je považovaná za poruchu, ale je nutné na ňu upozorniť, je keď sa niektoré koleso neotáča (jeho rýchlosť je 0.00). Ak jedna z týchto situácií nastane, je nutné vypísať správu, ako je popísané nižšie.
Špecifikácia vstupuVstup programu pozostáva z vopred neurčeného počtu návrhov súkolí, ktoré je treba analyzovať. Každý opis návrhu začína riadkom so šiestimi celými číslami: x, y, ir, or, w, n. Prvé dve čísla sú súradnice hnacieho kolesa x, y (1 <= x, y <=300); ďalšie dve sú veľkosti jeho vnútorného ir a vonkajšieho or polomeru (1 <= ir, or <= 100). Piate celé číslo je rýchlosť w (-1000 <= w <=1000) hnacieho kolesa v otáčkach za minútu (záporné číslo znamená otáčanie v protismere hodinových ručičiek a kladné číslo znamená otáčanie v smere hodinových ručičiek) a posledné šieste číslo v riadku n určuje počet ostatných kolies v súkolí, teda počet kolies okrem hnacieho kolesa (1 <= n <= 20). Ďalej nasleduje n riadkov obsahujúcich vždy štyri celé čísla charakterizujúce jednotlivé kolesá súkolia. Prvé dve čísla určujú súradnice xi, yi (1 <= xi, yi <=300) a druhé dve určujú veľkosti vnútorného iri a vonkajšieho ori polomeru kolesa (1 <= iri, ori <= 100). Vstup je ukončený hodnotami x = y = ir = or = w = n = 0.
Špecifikácia výstupuPre každý návrh má program vypísať buď zoznam kolies s ich rýchlosťami otáčania, alebo hlásenie o poruche. Prvý riadok výstupu má obsahovať len text „Sukolie X“, pričom X je poradové číslo súkolia (začínajúce od 1). Ak návrh neobsahuje ani jednu poruchu, ďalších n riadkov obsahuje vždy číslo kolesa (číslo je zarovnané doprava v stĺpcoch 1 a 2); v stĺpci 3 je dvojbodka nasledovaná medzerou, v 5. stĺpci je buď „P“ pre otáčanie v protismere hodinových ručičiek, alebo „S“ pre otáčanie v smere hodinových ručičiek. Od siedmeho stĺpca je napísaná veľkosť rýchlosti (v otáčkach za minútu) zaokrúhlená na dve desatinné miesta. Ak niektoré z kolies má nulovú rýchlosť, program má vypísať správu“ „koleso sa neotaca“. Správa začína v 5. stĺpci namiesto informácie o smere a veľkosti rýchlosti kolesa. Ak je v návrhu porucha, program má vypísať len prvý riadok obsahujúci „Sukolie X“ a druhý riadok obsahujúci jednu z dvoch správ. Ak dochádza k prekrytiu dvoch alebo viacerých kolies na vnútornej, alebo vonkajšej úrovni, program má vypísať: „Porucha -- prekrytie kolies“. Ak je niektoré koleso otáčané dvoma rozdielnymi rýchlosťami, správa je „Porucha -- konflikt otacania kolies“. Výstupy pre jednotlivé návrhy majú byť oddelené prázdnym riadkom.
Ukážkový vstup20 100 5 5 -300 5 43 100 18 10 43 74 8 4 71 100 10 15 94 100 3 8 122 100 25 6 20 100 5 5 -300 5 43 100 18 10 43 74 8 4 71 100 10 15 94 100 3 8 105 100 25 6 20 100 5 5 -300 5 43 100 18 10 43 74 8 4 71 100 10 15 94 100 3 8 125 100 25 6 0 0 0 0 0 0
Ukážkový výstupSukolie 1 1: S 83.33 2: P 187.50 3: P 150.00 4: S 281.25 5: P 33.75 Sukolie 2 Porucha -- prekrytie kolies Sukolie 3 1: S 83.33 2: P 187.50 3: P 150.00 4: S 281.25 5: koleso sa neotaca Problém B: Strašidelný dom(dom.c | .C | .p) Malý Janko má veľmi rád strašidelné rozprávky. Rád ich počúva, číta, ale najmä si ich rád vymýšľa. Veľký dom, v ktorom býva je pre neho vždy plný dobrých strašidielok, krásnych víl a hlavne zlých strašidiel schovaných v najtmavších kútoch domu. Raz sa Jankovi rodičia rozhodli ísť na večerné predstavenie do divadla. Janko ich presviedčal, že už je veľký a môže preto zostať sám doma. Sľúbil, že pozhasína všetky svetlá a bude sa hrať vo svojej izbe. Nanešťastie, dom, v ktorom Janko so svojimi rodičmi býva, bol postavený dosť avantgardne. Vypínače k lampám neboli umiestnené vždy v tej istej miestnosti ako lampy. Po tom, ako Janko vyprevadil svojich rodičov až do haly a počkal kým vyšli von, si uvedomil, že celý dom je ponorený do tmy, lebo všetky svetlá sú vypnuté. Len v hale, kde stál, bolo zažnuté. Janko sa musel vydať na cestu do svojej izby. V jeho predstavivosti ožívali tie najhoršie strašidlá a prízraky. V takomto strachu by Janko nikdy nevošiel do izby, kde by bolo zhasnuté a nikdy by si nezhasol v izbe, v ktorej práve bol. Po chvíli premýšľania si Janko uvedomil, že čudné umiestnenie vypínačov pre lampy môže využiť proti všetkým príšerám, ktoré sa v jeho predstavivosti báli svetla. Vymyslel plán, ako prejde do svojej izby tak, že nakoniec zostanú všetky lampy vypnuté, ako bolo zvykom v ich domácnosti, zažnuté zostane len v jeho izbe, kde počká na rodičov. Vašou úlohou je napísať program pre Janka, ktorý pre daný popis domu určí, ako sa dostane z haly do svojej izby, ak na začiatku je zažnuté len v hale. Janko nikdy nevojde do izby, kde sa nesvieti a po Jankovom poslednom kroku bude vo všetkých izbách okrem jeho izby zhasnuté. Ak vedie do miestnosti viac ciest, musíte vybrať tú cestu, ktorá obsahuje najmenej krokov, pričom za krok sa považuje „prechod z jednej izby do druhej“, „zažnutie svetla“ alebo „zhasnutie svetla“. Ak existuje takýchto najkratších ciest viac vypíšte ľubovolnú z nich.
Špecifikácia vstupuVstup obsahuje niekoľko popisov Jankovho domu. Každý popis začína riadkom obsahujúcim tri celé čísla i, d a v. Číslo i znamená počet izieb domu (1 <= i <= 10), d je počet dverí medzi izbami a v je počet vypínačov v dome. Izby sú číslované od 1 po i, izba číslo 1 je hala a izba číslo i je Jankova izba. Po tomto riadku nasleduje d riadkov obsahujúcich dve celé čísla k a l, ktoré určujú že medzi izbami k a l sa nachádzajú dvere. Potom nasleduje v riadkov obsahujúcich dve čísla m a n, určujúcich, že vypínač v izbe m ovláda lampu v izbe n. Popisy izieb oddeľuje prázdny riadok. Vstup končí riadkom s hodnotami i = d = v = 0, ktorý sa už nespracováva.
Špecifikácia výstupuPre každý dom, prvý riadok výstupu je tvaru „Dom X“, kde X je číslo domu v poradí (čísluje sa od 1). Ak pre Jankovu cestu existuje riešenie, výstup je najkratšia možná postupnosť krokov, ktoré vedú Janka z haly tak, aby sa na konci svietilo len v Jankovej izbe. (Ak je viac možných ciest, vypíšte ľubovolnú najkratšiu). Po prvom riadku označujúcom číslo domu, nasleduje riadok: „Janko sa dostane do izby na Y krokov:“, kde Y je počet krokov, na ktoré sa Janko do svojej izby dostane. Každý z Y krokov je zapísaný v jednom riadku a výpis sa začína až od druhého stĺpca. Pre prejdenie do izby i, vypíše sa správa „- Prejdi do izby i.“, pre zažnutie svetla v izbe i sa vypíše správa: „- Zazni svetlo v izbe i.“ a pre zhasnutie svetla v izbe i sa vypíše správa: „- Zhasni svetlo v izbe i.“. Ak cesta neexistuje, vypíše sa správa: „Jankov problem sa neda vyriesit.“. Výstupy pre jednotlivé domy majú byť oddelené prázdnym riadkom.
Ukážkový vstup3 3 4 1 2 1 3 3 2 1 2 1 3 2 1 3 2 2 1 2 2 1 1 1 1 2 0 0 0
Ukážkový výstupDom c.1 Janko sa dostane do izby na 6 krokov: - Zazni svetlo v izbe 2. - Zazni svetlo v izbe 3. - Prejdi do izby 2. - Zhasni v izbe 1. - Prejdi do izby 3. - Zhasni svetlo v izbe 2. Dom c.2 Jankov problem sa neda vyriesit. Problém C: Spravodlivosť(spravod.c | .C | .p) V malom štátiku na ostrove v Tichomorí sa po reforme súdnictva zmenil spôsob rozhodovania v súdnych sporoch. Rozhodnutia sú teraz určované porotou pozostávajúcou z ľudu. Vždy, keď sa začína nejaký súdny spor, vyberie sa porota. Najprv sa náhodne vyberie niekoľko ľudí – kandidátov na porotcov. Každému vybranému človeka, priradí obžaloba aj obhajoba známku od 0 do 20, ktorá znamená ich preferenciu pre toho človeka. 0 znamená, že človek sa na spor vôbec nehodí, 20 znamená, že človek je pre spor vybraný ideálne. Z týchto známok od obhajoby a obžaloby vyberie sudca porotu. Aby zabezpečil čo najspravodlivejší proces, snaží sa vybrať porotu tak, aby bola spokojnosť obhajoby aj obžaloby rovnaká. Sudca teda vyberá porotu tak, aby vyhovovala obom stranám približne rovnako. Výber porotcov teda prebieha takto: je daných n náhodne vybraných potenciálnych porotcov a dve hodnoty hi (známka obhajoby) a zi (známka obžaloby) pre každého potenciálneho porotcu I; úlohou je vybrať m porotcov. Nech porota P je podmnožina množiny {1, …, n} s m prvkami, potom H(P) je suma hi pre všetky i patriace P (celková hodnota známok obhajoby pre m porotcov) a Z(P) je suma zi pre všetky i patriace P (celková hodnota známok obžaloby pre m porotcov). Optimálna porota P má minimálnu hodnotu |H(P) – Z(P)|. Ak je viac možných porôt, ktoré spĺňanú túto podmienku, vyberie sa taká, ktorá najviac vyhovuje obžalobe aj obhajobe, teda taká, ktorá maximalizuje hodnotu H(P) + Z(P). Vašou úlohou je napísať program, ktorý vykonáva tento spravodlivý výber porotcov a vyberá z daných kandidátov optimálnu porotu.
Špecifikácia vstupuVstup obsahuje opísané situácie niekoľkých procesov. Každý opis situácie pre proces začína riadkom obsahujúcim dve celé čísla n a m, kde n je počet kandidátov (1<= n <= 200) a m je počet členov poroty (1 <= m <= 20), pričom m < n. Nasleduje n riadkov obsahujúcich dve celé čísla hi a zi pre i = 1, …, n. Vstup sa končí situáciou majúcou n = m = 0, ktorá sa nespracováva.
Špecifikácia výstupuPre každú situáciu, prvý riadok výstupu obsahuje text „Porota X“, kde X je číslo situácie (poroty) v poradí (čísluje sa od 1). Druhý riadok bude obsahovať text “Najlepsia porota ma hodnotu Z(P) pre obzalobu a hodnotu H(P) pre obhajobu:”, kde H(P) a Z(P) sú konkrétne číselné ohodnotenia pre vybranú porotu. Ďalší riadok bude obsahovať m poradových čísel vybraných kandidátov zoradených vzostupne. Pred každým číslom kandidáta poroty je na výstupe práve jedna medzera. Po každej situácii vypíšte prázdny riadok. Ukážkový vstup4 2 1 2 2 3 4 1 6 2 0 0
Ukážkový výstupPorota c.1 Najlepsia porota ma hodnotu 6 pre obzalobu a hodnotu 4 pre obhajobu: 2 3 Problém D: Falošná minca(minca.c | .C | .p) Rastislav dostáva za svoju prácu v kováčskej dielni každý mesiac 12 zlatých dukátov. Jeho majster je však veľmi lakomý a namiesto 12 zlatých dukátov mu vždy dá len 11 pravých dukátov a 1 mincu, ktorá vyzerá na pohľad rovnako, ale nie je pravá. Vždy sa líši svojou váhou a keďže falošné mince majster vyrába vždy potajomky a narýchlo, niekedy je falošná minca ťažšia ako pravá, inokedy ľahšia. Rastislav vždy vie, že jedna minca je falošná (vie, že majstrovo svedomie mu nedovolí viac okrádať svojich zamestnancov), ale nevie, či je ťažšia, alebo ľahšia ako pravý dukát. Rastislavov priateľ má veľmi presné váhy, čo je veľká vzácnosť v celom chotári. Pretože je na ne veľmi pyšný, dovoľuje Rastislavovi v jednom mesiaci len tri váženia. Keď teda Rastislav dostane na konci mesiaca odmenu za svoju prácu v kováčskej dielni, ide za svojím priateľom a urobí tri váženia. Napríklad, keď Rastislav odváži dve mince a váhy ukazujú, že sú rovnaké, vie, že obe sú pravé zlaté dukáty. Teraz, ak odváži jednu z týchto dvoch pravých mincí s treťou mincou a váhy sa vychýlia, Rastislav vie, že tretia minca je falošná a vie aj to, či je ľahšia, ako pravé dukáty, alebo ťažšia. Rastislav vyberá mince na váženie pozorne – vždy je schopný zaistiť, že po troch váženiach nájde falošnú mincu.
Špecifikácia vstupuPrvý riadok obsahuje celé číslo n (1 <= n <= 1000) určujúce počet prípadov, ktoré nasledujú. Každý prípad pozostáva z troch riadkov vstupu, každý jeden je pre jedno váženie. Rastislav si označil svoje mince písmenami A-L. Informácie o váženiach sú určené dvomi reťazcami znakov a jedným zo slov „hore“, „dole“ alebo „vyrovnana“. Prvý reťazec znakov reprezentuje mince na ľavej miske váhy; druhý reťazec reprezentuje mince na pravej miske váhy. (Rastislav dáva vždy rovnaký počet mincí na ľavú i pravú misku váh.) Slovo na tretej pozícii hovorí, či pravá strana váh ide hore, dole, alebo zostala vyrovnaná. Vstupy sú zadané tak, že sa dá vždy odhaliť falošná minca, pričom falošná minca je vždy práve jedna.
Špecifikácia výstupuPre každý prípad je výstup tvorený jedným riadkom, v ktorom je veta „X je falosna minca a je Y.“, kde X je veľké písmeno A-L a určuje, ktorá minca je falošná. Y je jedno zo slov „lahsia“ a „tazsia“. Ukážkový vstup1 ABCD EFGH vyrovnana ABCI EFJK hore ABIJ EFGH vyrovnana
Ukážkový výstupK je falosna minca a je lahsia. Problém E: Potopa(potopa.c | .C | .p) Istá pochybná realitná spoločnosť prišla s geniálnou myšlienkou ako dobre zarobiť na bezcenných pozemkoch. Ponúka svojim klientom za neuveriteľné akciové ceny pozemky v krásnej lokalite malebného údolia, ktoré však – a v tom je ten háčik – býva nezriedka z veľkej časti úplne zatopené vodou. S kvalitným poistením proti vytopeniu to však môže byť celkom výhodná investícia. Pre určenie výšky poistného je však nevyhnutné určiť do akej výšky môže voda pri daných zrážkach v zatopenom údolí vystúpiť. O regióne údolia sú k dispozícii kompletné zemepisné údaje s vyvýšením každého štvorca územia s rozmermi 10 x 10 metrov. Dažďová voda a voda z topiaceho sa snehu sa najskôr zhromažďuje v štvorcoch s najnižšou výškou a postupne zaplavuje štvorce nachádzajúce sa vyššie a vyššie. Pre jednoduchosť predpokladajme, že časté búrky so silným vetrom umožnia, aby sa voda z vyšších štvorcov vždy dostala do nižšie položených štvorcov a nikdy sa nestane, aby uviazla lokálnych preliačinách. Taktiež predpokladáme, že pôda v krajine vodu vôbec neabsorbuje a že voda sa nemôže nikdy vyliať do okolitej krajiny mimo zadaného regiónu. Vašou úlohou je napísať program, ktorý pre zadané množstvo vody v krajine vypočíta do akej výšky vystúpi vodná hladina v údolí, keď bude postupne zaplavovať najnižšie položené štvorce v krajine a aká časť územia bude nakoniec pod vodou (to znamená určiť koľko percent štvorcov má výšku ostro menšiu ako je výška vodnej hladiny).
Špecifikácia vstupuVstup pozostáva z postupností opisov viacerých údolí. Každý opis začína dvojicou celých čísel m a n (1 <= m, n <= 30) určujúcimi obdĺžnikové rozmery územia v 10-metrových jednotkách. Nasleduje m riadkov obsahujúcich n hodnôt výšok jednotlivých štvorcov. Výšky sú kladné a záporné celé čísla určujúce nadmorskú výšku v metroch (-1000 .. +1000). Poslednou hodnotou každého opisu je celé číslo určujúce množstvo nazbieranej vody v kubických metroch (0 .. +1000000). Hodnoty n = m = 0 signalizujú koniec vstupu.
Špecifikácia výstupuPre každý opis, prvý riadok výstupu obsahuje text „Udolie X“, kde X je číslo opisu údolia v poradí (čísluje sa od 1). Druhý riadok bude obsahovať text „Vyska vodnej hladiny je Y metrov.“, kde Y je výška hladiny zaokrúhlená na 2 desatinné miesta (%.2f). Tretí riadok bude obsahovať text „Z % udolia je pod vodou.“, kde Z vyjadruje časť zaplavenej krajiny zaokrúhlenú na 2 desatinné miesta (%.2f). Medzi výstupmi pre jednotlivé regióny vynechajte jeden prázdny riadok. Ukážkový vstup3 3 25 37 45 51 12 34 94 83 27 10000 0 0
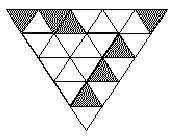
Ukážkový výstupUdolie 1 Vyska vodnej hladiny je 46.67 metrov. 66.67 % udolia je pod vodou. Problém F: Trojuholník(trojuhol.c | .C | .p) Keďže sa blížia Vianoce, rodičia poverili malého Janka úlohou, aby zhotovil veľkú hviezdu, ktorá sa potom nastokne na vrchol vianočného stromčeka. Ale keď si Janko zobral do rúk papier, zistil, že sa v ňom nachádza viacero dier. To si zlé strašidlá z najtmavších kútov domu povystrihovali drobné trojuholníčky na hviezdy pre vlastné vianočné stromčeky. Preto Janko potrebuje vašu pomoc. Vašou úlohou je napísať program, ktorý pre zadanú trojuholníkovú štruktúru pozostávajúcu z bielych a čiernych (dier) trojuholníčkov zistí, aká je plocha najväčšieho súvislého trojuholníka pozostávajúceho iba z bielych trojuholníčkov vo vnútri tejto štruktúry. Najväčší trojuholník môže mať svoj “vrchol” otočený buď nahor alebo nadol. Obrázok k 1. situácii z ukážkového vstupu:
Špecifikácia vstupuVstup pozostáva z opisov viacerých trojuholníkových štruktúr. Prvý riadok každého opisu obsahuje celé číslo n (1 <= n <= 100), ktoré určuje výšku trojuholníkovej štruktúry. Každý z nasledujúcich n riadkov obsahuje množinu znakov { medzera, #, – } reprezentujúcu jeden riadok trojuholníkovej štruktúry. Pričom znak ‘#’ predstavuje čierny a znak ‘–’ biely trojuholníček. Medzery sú použité iba na zarovnanie riadku, aby bol dodržaný trojuholníkovitý tvar celej štruktúry. Pre trojuholníkovú štruktúru je počet znakov ‘#’ a ‘–’ v každom riadku vždy nepárny a znižuje sa od hodnoty 2*n-1 až po hodnotu 1. Hodnota n = 0 signalizuje koniec vstupu.
Špecifikácia výstupuPre každý opis, prvý riadok výstupu obsahuje text „Trojuholnik X“, kde X je poradové číslo trojuholníkovej štruktúry (čísluje sa od 1). V druhom riadku je text „Plocha najvacsieho trojuholnika je Y.“, kde Y je počet bielych trojuholníčkov, z ktorých pozostáva najväčší trojuholník. Medzi výstupmi pre jednotlivé štruktúry vynechajte jeden prázdny riadok. Ukážkový vstup
5
#-##----#
-----#-
---#-
-#-
-
4
#-#-#--
#---#
##-
-
0
Ukážkový výstupTrojuholnik 1 Plocha najvacsieho trojuholnika je 9. Trojuholnik 2 Plocha najvacsieho trojuholnika je 4. Problém G: Permutácie(permut.c | .C | .p) Zo zadaného reťazca znakov môžeme poprehadzovaním jeho jednotlivých písmen vytvoriť nový reťazec. Ak na množine znakov zavedieme konkrétne usporiadanie, potom môžeme všetky reťazce, ktoré dostaneme jednoduchými výmenami písmen, usporiadať a každému reťazcu vieme jednoznačne priradiť číslo podľa jeho poradia v tomto usporiadaní. Napríklad pre abecedné usporiadanie a reťazec „bcba” existuje 12 rôznych permutácií, ktorým dokážeme takto priradiť čísla podľa ich poradia:
Preto pozícia reťazca „bcba” v postupnosti jeho permutácií je 9. Vašou úlohou je napísať program, ktorý pre zadaný reťazec znakov určí jeho pozíciu v abecedne usporiadanej postupnosti jeho vlastných permutácií. Počet permutácií môže byť veľmi veľké číslo, ale nikdy nepresiahne hodnotu 231 – 1.
Špecifikácia vstupuVstup pozostáva z postupnosti reťazcov, pričom každý reťazec sa nachádza na samostatnom riadku. Každý reťazec pozostáva maximálne z 30 malých písmen (‘a’ .. ‘z’). Vstup bude ukončený reťazcom „#”.
Špecifikácia výstupuVýstup obsahuje pre každý vstupný reťazec poradové číslo tohoto reťazca v postupnosti permutácií. Každý riadok výstupu obsahuje jedno číslo zarovnané doprava na 10 miest (%10d). Ukážkový vstupabcbb bcd dcb #
Ukážkový výstup
3
1
6
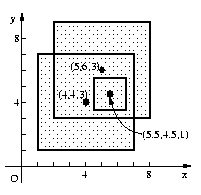
Problém H: Pokrytie(pokrytie.c | .C | .p) Istá oceliarska spoločnosť si vymyslela veľmi netradičný spôsob, ktorým sa rozhodla upútať pozornosť jedného zo svojich permanentných neplatičov. Jednu z mnohých zásielok oceľových plechov sa rozhodla zložiť priamo na udržiavaný trávnik rovno pred sídlo spoločnosti tohoto neplatiča. Bolo z toho samozrejme veľké haló a vlastne sa tým ani nič nedosiahlo, ale aspoň sa na tom nabalili právnické firmy zastupujúce obe spoločnosti. Právnici oboch spoločností ešte niekoľko nasledujúcich týždňov chodili po doničenom trávniku a snažili sa odhadnúť výšku takto vzniknutej škody. Pre tento účel je potrebné, aby ste napísali program, ktorý určí plochu zničeného trávnika. Úlohou je teda zistiť veľkosť plochy, ktorú pokrývajú cez seba poukladané plechy. Každý plech je štvorcového tvaru a je pre neho zadefinovaný jeho stred (xi, yi) a jeho “polomer” (r = kolmá vzdialenosť od stredu k ľubovolnému okraju). Obrázok k 1. situácii z ukážkového vstupu:
Špecifikácia vstupuVstup pozostáva z postupnosti opisov rozloženia jednotlivých plechov. Prvý riadok každého opisu obsahuje celé číslo n (2 <= n <= 100) určujúce počet plechov. Nasledujúcich n riadkov obsahuje definície konkrétnych plechov. Každý z týchto riadkov obsahuje 3 reálne čísla: súradnice stredu x, y a polomer r (0.0 <= x, y, r <= 200.0). Hodnota n = 0 signalizuje koniec vstupu.
Špecifikácia výstupuPre každý opis na vstupe obsahuje výstup 2 čísla oddelené jednou medzerou. Prvé číslo je poradové číslo konkrétneho opisu a druhé číslo určuje celkovú plochu prekrytej oblasti trávnika. Hodnota plochy je zaokrúhlená na 2 desatinné miesta (%.2f). Ukážkový vstup3 4.0 4.0 3.0 5.0 6.0 3.0 5.5 4.5 1.0 2 3.0 3.0 3.0 1.5 1.5 1.0 0
Ukážkový výstup1 52.00 2 36.00 |