Plánovanie dôkazov pomocou znalostí
Gabriel Pap
Katedra informatiky a výpočtovej techniky
Ilkovičova 3, 831 02 Bratislava, Slovenská republika
pap@decef.elf.stuba.sk
Spracované podľa: E. Melis, J. Siekmann: Knowledge-based proof
palnning, Artificial Intelligence 11, pp. 65-100, 1999
Abstrakt
Plánovanie dôkazov pomocou znalostí je
novou paradigmou v automatizovanom dokazovaní viet. Používa a ďalej
rozvíja veľa princípov a techník umelej inteligencie, ako hierarchické
plánovanie, reprezentácia znalostí v rámcoch, riadiace pravidlá, riešenie
obmedzení, taktické uvažovanie a uvažovanie na meta úrovni. Líši sa od
klasických prehľadávacích techník
v automatizovanom dokazovaní viet najmä svojou abstrakciou. Dôkaz vety je
naplánovaný na abstraktnej úrovni a obrys dôkazu je nájdený. Tento
abstraktný plán dôkazu môže byť rekurzívne rozvinutý až na dôkaz na úrovni
logického počtu. Operátory plánu predstavujú matematické techniky používané
matematikmi. Znalosti sú špecifické pre danú oblasť matematiky, ale
reprezentačné techniky a uvažovacie procedúry sú všeobecného charakteru.
Všeobecný plánovač používa tieto znalosti spolu s deklaratívne reprezentovanými
riadiacimi pravidlami, ktoré zodpovedajú matematickej intuícii, na nájdenie
dôkazu vety. Tieto pravidlá sú základom pre uvažovanie na meta úrovni
a cieľom riadeného správania.
Kľúčové slová: dokazovanie viet, plánovanie, automatizované
plánovanie dôkazov, meta úrovňové uvažovanie.
Abstract (in english)
Obsah
-
3.3.1 Klasické automatizované dokazovače
viet a rozhodovacie procedúry
-
3.3.2 Výpočtové algebraické systémy
1 Úvod
Automatizované dokazovanie viet ... to nie je ten krásny proces, ktorí
poznáme ako matematici. To je ‘zavri si oči a hľadaj zrnko kukurice diamantového
tvaru v kukuričnom poli’.
Matematici nám ukázali správny smer za posledné dve, alebo tri tisícročia.
Venujme tomu dostatočnú pozornosť.
Woody Bedsoe, 1986
Od počiatku výskumu umelej inteligencie, existovali dve školy
v oblasti automatizovaného dokazovania viet (Automated theorem proving –
ATP), logicky orientovaný prístup a skôr psychologicky orientovaný
prístup, ktorý sa snaží simulovať správanie ľudí. Na konferencii
v Dartmouth-e v roku 1956 si získali veľkú pozornosť dva systémy
a sú pokladané za „klasické“ v súčasnosti: rozhodovacia procedúra
Martina Davisa, založená na Presburgerovej aritmetike, ktorá je predchodcom logicky orientovaných
systémov a logický teoretik, ktorý sa stal priekopníkom druhej kategórie.
V roku 1954 Davisov systém bol vôbec prvý systém, ktorý dokázal pomocou
počítača matematickú vetu („Suma dvoch párnych čísiel je párna“)
a o rok neskôr, Allan Newell a Herb Simon dokončili svoj
spoločný systém, neskôr nazvaný logický teoretik, ktorý uspel v dokazovaní
mnohých viet a oslnil tak túto oblasť umelej inteligencie.
S objavením rezolvenčného pravidla v roku 1965, logicky
orientovaná paradigma založená na prehľadávaní sa stala dominantnou
v oblasti automatizovaného dokazovania viet a najvýkonnejšie systémy
boli skonštruované v tomto duchu.
Iné nápady však nikdy nechýbali. Woody Bledsoe, medzi ostatnými sa zaslúžil
o ATP založené na matematických znalostiach a skúsenostiach.
Horeuvedená Bledsoe-ová krásna myšlienka ukazuje jeho skepticizmus pre
dokazovanie viet založené výhradne na prehľadávaní. Nikdy neveril, že len
pomocou prehľadávania by sa dali úspešne dokázať zložité vety aj z dobre
pochopených oblastí matematiky.
Pôvodné automatizované dokazovanie viet je založené na strojovo
orientovanom logickom počte ako je rezolvečný kalkulus, alebo maticové metódy.
Inferenčné pravidlá takýchto počtov obopínajú prehľadávací priestor
a viac než tridsať rokov výskumu viedlo k zlepšovaniu stratégií
prehľadávania týchto obrovských (viac než bilión uzlov) priestorov. Inferenčné
kroky definované pomocou týchto počtov sú skôr malé a nízko-úrovňové, keď
ich porovnávame s dôkazovými krokmi skúseného matematika.
Pôvodné systémy ako MKRP, OTTER, SETHEO alebo SPASS, sú v podstate
čierne skrinky, ktorých vstupom je veta a presne tie axiómy, ktoré sú
potrebné na dôkaz vety. Po nastavení príslušných parametrov, systém slepo hľadá
postupnosť logických pravidiel, ktoré by dokázali vetu na základe vstupných
axiómou. Prehľadávanie je podporované všeobecným riadením, nazývaným stratégia
alebo zjemňovanie, ktoré je čisto syntaktické a ťažko odzrkadľuje
matematický spôsob objavenia dôkazu.
Tieto systémy ťažia z technologického pokroku v oblasti vývoja
rýchlejších počítačov s veľkou úložnou kapacitou. Dokážu uskladniť
a prehľadať milióny klauzúl a vskutku to aj robia. Vďaka tomuto
pokroku a lepšej reprezentácie problémov, nadobudli tieto systémy pozoruhodnú silu a sú schopné dokázať aj netriviálne matematické problémy,
ktorých dôkazy sú často neintuitívne, zložité a práve preto skryté pre
ľudí. Vo všeobecnosti však väčšina dôkazov je
jedinečný matematický problém aj v dobre pochopených oblastiach
a je ďaleko za možnosťami ktoréhokoľvek z dnešných systémov.
A práve preto, po štyridsiatich rokoch výskumu je čas spýtať sa otázku :
„Sme na zlej ceste?“
1.1 Psychológia matematického objavu
Ako dokáže matematik narábať s dlhými a komplexnými dôkazmi
a čo je jeho stratégia pri vyhýbaní sa menej sľubným dôkazovým cestám?
Ak vychádzame z doterajších znalosti o našich intelektuálnych
schopností, nevieme odpovedať na túto otázku. Predsa aspoň nasledujúce tri
pozorovania sú všeobecne prijaté:1) zmýšľanie matematika často nie je založené
na konkrétnej, jasnej reprezentácie problému. 2) Zložité vety nie sú dokázané
priamo, ale častejšie použitím známych dôkazových techník, ako indukcia, dôkaz
diagonilizáciou a pod. V skutočnosti dobrý matematik pozná niekoľko
tuctov (ale pravdepodobne menej ako tisíc) dôkazových techník vo svojej oblasti
výskumu. Tiež má k dispozícii tisíce menších matematických trikov ako a kedy
použiť homomorfizmus, kedy derivovať,
ako reformulovať problém. Je nepredstaviteľné aby toto všetko sa dalo dosiahnuť
len pomocou prehľadávania. Pre veľmi zložité a otvorené matematické
problémy, otvorené práve preto lebo žiadna zo známych techník nevedie
k výsledku, je potreba poprehadzovať tieto štandardné techniky
a preto po tretie je tu empirický dôkaz, ktorý naznačuje, že
matematici plánujú dôkaz na rôznych
úrovniach abstrakcie v procese objavenia dôkazu.
Dôkazové plány majú svoje opodstatnenie a v nasledujúcich dvoch
kapitolách by som rád spomenul dve oblasti výskumu, ktoré tiež majú osoh
z tohto nového pohľadu, t.j. z faktu že existuje dobre definovaná
konkrétna reprezentačná úroveň nad úrovňou logického počtu.
1.2 Dôkazy analógiou
Dôkazy viet pomocou analógie je malou podoblasťou automatizovaného dokazovania viet. Často môžeme nájsť dva
analogické dôkazy, avšak ťažké je nájsť určité spojenie medzi syntaktickou
reprezentáciou zdrojového dôkazu a cieľového, preto techniky založené na
mapovaní sú neúspešné. Principiálne je dôkazová idea rovnaká, ale detaily
zdrojového a cieľového dôkazu sa môžu líšiť. Napríklad, nie každý detail
dôkazu LIM+ (limita sumy dvoch funkcií sa rovná sume jednotlivých limít
funkcií) sa môže preniesť na dôkaz LIM* (limita súčinu dvoch funkcií sa rovná
súčinu limít jednotlivých funkcií), aj keď dôkazy týchto dvoch viet sú veľmi
podobné a je možné uskutočniť určité mapovanie medzi nimi.
Ako potom dokážeme uhádnuť správnu mieru abstrakcie ak to nie je na úrovni
logického počtu. Dôkazové plány sú oveľa abstraktnejšie ako dôkazy na úrovni
logického počtu a často umožňujú explicitne zachytiť podstatnú myšlienku
dôkazu.
1.3 Plánovanie dôkazov
Plánovanie dôkazov bolo pôvodne dosiahnuté rozšírením taktického
dokazovania viet. Taktické dokazovanie viet je založené na zápise taktiky,
ktorá v sebe zapúzdruje opakujúce sa postupnosti inferenčných krokov do
makro-krokov. Tieto taktiky sú potom vykonané príslušným programom, čo má za
následok vykonanie postupnosti niekoľkých dôkazových krokov na úrovni logického
počtu. Užívateľ potom nemusí použiť príliš veľký počet jednoduchých
inferenčných pravidiel pri interaktívnom dokazovaní viet.
Princíp plánovania dôkazov je nasledujúci. Reprezentácia dôkazu pozostáva
z postupnosti komplexných operátorov, akými sú napríklad použitie
homomorfizmu, rozvitie definície, aplikácia lemy, niekoľko zjednodušení, alebo
derivácia funkcie. Každý z týchto operátorov, nazývaných metódy, môže byť
v princípe rozvinutý do postupnosti inferenčných krokov pomocou taktiky. Keď
teraz každá z týchto taktík je vyhodnotená pomocou pre-
a postconditionu (predpokladu a dôsledku), môžeme plánovať postupnosť
taktík. Toto spojenie plánovacích operátorov a taktík bola Alan Bundyho
kľúčová myšlienka plánovania dôkazov.
Nedávno ďalší typ metód s rozvinutou schémantikou bol definovaný.
Metódy nie sú obmedzené na ich taktický
pôvod, ale môžu byť definované viac všeobecne ako operátory plánovania dôkazu,
t.j. ako stavebné kamene pre plán dôkazu, ktoré môže byť rekurzívne rozvinuté
na úroveň logického dôkazu.
Plánovanie dôkazu hľadá plán, takú postupnosť metód pre ktoré predpoklady
(precondition) metódy sa zhodujú s dôsledkom (postcondition) predchodcu
v tejto postupnosti. Tento dobre známy pohľad na plán prirodzene vedie
k novému spôsobu automatizovaného dokazovania viet. Plánovač môže byť
použitý na plánovanie postupnosti metód ktoré transformujú predpoklady dôkazu
do vety. Toto umožňuje použitie aj
štandardných heuristík a techník z literatúry o plánovaní.
Plánovanie dôkazov takto poskytuje spôsob kontroly globálneho
prehľadávania, ktorá zodpovedá matematickej intuícii, na rozdiel od lokálnych
a syntaktických prehľadávacích heuristík, ktoré sa bežne používajú
v klasickom automatizovanom dokazovaní viet.
Tento článok rozširuje plánovanie dôkazov na plánovanie pomocou znalostí.
V nasledujúcej kapitole opisuje aké znalosti sú k dispozícii
v matematike a ako môžu byť reprezentované. Tretia kapitola opisuje
ako môže všeobecný plánovač dôkazov využiť matematické znalosti ako metódy, riadiace
pravidlá a externé uvažovacie
systémy. Niekoľko techník je predstavených, ktoré obmedzujú prehľadávanie pri
plánovaní dôkazov. V kapitole 3.2 je to
uvažovanie na meta úrovni a v kapitole 3.3 externé uvažovacie
systémy.
2 Princípy plánovania dôkazov
Táto kapitola v krátkosti opisuje notácie používané v oblasti
plánovania v umelej inteligencii a postupne predstavuje plánovanie
dôkazov pomocou tejto notácie. Rozšírenia k tu popísaným technikám ktoré
viedli k plánovaniu dôkazov pomocou znalostí sú opísané v kapitole
3. Na zápis substitúcie používam s a na skrátenie výsledku použitia s na F - Fs.
2.1 Základy plánovania
Problém plánovania pozostáva z počiatočného stavu, opisujúceho
východiskovú situáciu a z cieľov, ktoré chceme dosiahnuť. Oblasť (doména) plánovania je definovaná
pomocou operátorov, ktoré reprezentujú nejaké akcie. Operátory majú
špecifikácie, ktoré sa použijú v plánovacom procese. V notácii
používanej systémom STRIPS sa tieto špecifikácie nazývajú predpoklady
a efekty. Predpoklady špecifikujú podmienky stavu plánovania, ktoré chceme
dosiahnuť, aby bolo možné použiť operátor. Pričom efekty opisujú potencionálne
zmeny v stave plánovania spôsobené použitím tohto operátora.
V notácii STRIPS sú efekty reprezentované ako pridaj-zoznamy (/) a zmaž-zoznamy (0), t.j. zoznamy znakov, ktoré sú pridané,
alebo zmazané aplikáciou operátora.
Čiastočný plán je čiastočne zoradená postupnosť krokov, (čiastočne)
vytvorených operátorov s ďalšími vopred zadanými obmedzeniami, alebo
vonkajšími obmedzeniami. Na čiastočný plán sa môžeme pozerať ako na implicitnú
reprezentáciu množiny postupností (množinu potencionálnych riešení) spolu zo
zoradením a vonkajšími obmedzeniami. Riešením plánovacieho problému je
celkový plán, ktorý zoradí (linearizuje) čiastočný plán a transformuje počiatočný
stav do cieľového stavu.
Operácie plánovača opakovane zjemňujú čiastočný plán, pridávajú kroky
a obmedzenia a takto zužujú množinu potencionálnych riešení, kým sa
z nej nedá vybrať riešenie. Tabuľka č. 2.1.1 ukazuje zjednodušený spätný
plánovací algoritmus. Plánovanie vychádza z čiastočného plánu o0 definovaného problémom, ktorý treba vyriešiť, pričom o0 pozostáva z krokov t0 až tº, ktoré sú konkrétnou reprezentáciou operátorov začiatok a koniec. Majú počiatočný stav ako /-efekty a ciele ako predpoklady, respektívne o0 tiež reprezentuje obmedzenie poradia t0
< tº. Zavedenie kroku do čiastočného plánu
odstráni nevyriešený cieľ g z cieľovej agendy G a môže spôsobiť
zavedenie nových podcieľov alebo obmedzení. S týmto zjemňovaním sa
pokračuje pokiaľ žiadny nevyriešený cieľ nezostal a našlo sa riešenie, alebo
neexistuje ďalší operátor ktorý je aplikovateľný.
Tabuľka 2.1.1 – Kostra spätného plánovania
Spätne-Zjemnuj-Plán(o,G)
Ukončenie: if cieľová agenda G prázdna, then Riešenie
if žiadny operátor sa nedá použiť, then
Neúspech
Výber cieľa: Vyber nevyriešený cieľ gcG,
Výber
operátora:
- Pre každý operátor M
pre každý /-efekt e z M
nech s je také, že platí es = g
if
podmienky-použitia(Ms) = true,
then
M je aplikovateľné.
- Vyber jeden použiteľný M
- vlož M do o
- vlož obmedzenia do o
- obnov G.
Rekurzia: Zavolaj Spätne-Zjemnuj-Plán na zjemnenom
čiastočnom pláne o.
Prehľadávanie je zahrnuté v každom z plánovacích algoritmov.
Proces plánovania pozostáva z postupnosti výberov, ktoré vedú k celkovému
plánu. Tieto rozhodnutia zahŕňajú výber nevyriešeného cieľa, ktorý sa má
najbližšie splniť a ktorý plánovací operátor použiť na dosiahnutie tohto cieľa.
Tieto rozhodnutia ovplyvňujú spôsob akým je priestor prehľadaný, alebo
obmedzený. Niektoré plánovače používajú explicitne deklarované riadiace
pravidlá na riadenie prehľadávania.
Po tomto krátkom prehľade klasického plánovania v umelej inteligencii
sa pozrieme na plánovanie dôkazov.
2.2 Plánovanie dôkazov
Plánovanie dôkazov berie plánovanie dôkazu ako plánovací problém. Je to
vlastne aplikácia plánovacích techník na matematiku. Táto oblasť obsahuje veľmi
komplexné problémy s potencionálne do nekonečna sa vetviacim prehľadávacím
priestorom. Konkrétny plánovací algoritmus nie je dôležitý z hľadiska
tohto článku, preto sa odkazujem na plánovač dôkazov používajúci jednoduchý
spätný a dopredný plánovací algoritmus, rozšírený o hierarchické
plánovanie.
Východiskový stav v plánovaní dôkazov je kolekcia dôsledkov,
dôkazových predpokladov a cieľ je dôsledok, ktorý chceme dokázať. Doména
plánovania dôkazov pozostáva z metód, riadiacich pravidiel
a uvažovacích systémov . Čiastočný plán dôkazu je čiastočne
zoradená množina metód a celkový, t.j. úplne rozvinutý dôkazový plán je
postupnosť jednoduchých metód, ktoré transformujú východiskový stav do
cieľového. Celkový plán je riešenie problému, samotný dôkaz vety.
Krása tohto prístupu spočíva v tom, že metódy predstavujú známe
matematické dôkazové techniky alebo často sa vyskytujúce operácie
s formulami. Vo všeobecnosti by metódy mali zachytiť
1)
spoločné
vzory v dôkazoch, t.j. spoločné štruktúry ako v dôkazoch pomocou
matematickej indukcie, alebo
2)
spoločné
dôkazové procedúry ako je zjednodušenie výrazov, alebo napríklad aplikácia hlavnej vety teórie čísiel (každé
prirodzené číslo sa dá zapísať ako súčet prvočísiel).
Východiskový stav v plánovaní dôkazov je zbierka dôkazových
predpokladov formálne zapísaných ako logické dôsledky pomocou jazyka na úrovni
objektov a cieľ je dôsledok, ktorý treba dokázať. Napríklad, pre dôkaz
vety LIM+ je cieľ
Æd![]()
a počiatočný stav sa skladá z nasledujúcich predpokladov
Æd![]()
Æd![]()
a z axiómou a definícií teórie o reálnych číslach.
Plánovanie dôkazu vychádza z čiastočného plánu o0 definovaného predpokladmi dôkazu a vety,
ktorú treba dokázať a hľadá riešenie problému. Čiže, postupnosť metód
ktoré transformujú počiatočný stav do cieľového stavu. WMEGov plánovač prehľadáva stavový priestor
pomocou spätného plánovania z cieľového a pomocou cieľovo
orientovaného dopredného plánovania z predpokladov.
WMEGA je komplexný systém slúžiaci na dôkaz
viet. A to aj interaktívneho alebo automatizovaného dokazovania viet. Jeho
distribuovaná architektúra integruje viacero (matematických) služieb, ako je
plánovač dôkazov, klasické automatizované dokazovače viet, bázu znalostí,
počítačové algebraické systémy a grafické rozhranie. V nasledujúcom
sa obmedzím na popis len tých vlastností tohto systému, ktoré sú dôležité
z hľadiska plánovania dôkazov pomocou znalostí. Bližšie informácie sú
uvedené v [2].
WMEGA používa hierarchické techniky plánovania a to abstrakciu operátorov
a abstrakciu predpokladov. Zovšeobecnenie plánovania abstraktných
operátorov umožňuje, že komplexné metódy môžu byť rozvinuté rekurzívne do
primitívnych metód, ktoré reprezentujú inferečné kroky na úrovni logického
počtu. Každé takéto rozvinutie je uchované v hierarchicky organizovanej
údajovej štruktúre o pláne dôkazu (Proof plan data structure – PDS), ako
je vidno z obrázka 2.2.1.
PDS slúži na reprezentáciu rôznych úrovní abstrakcie dôkazu. Východisková
PDS obsahuje východiskový plán o0 a postupne ako je tento plán zjemnený,
viacero uzlov je pridaných do PDS. Rozvinutie uzla pomocou metódy ho rozvinie
na podplán na ďalšej, nižšej úrovni abstrakcie.
Na obrázku 2.2.1 sú zobrazené tri úrovne abstrakcie. Na ľavej strane je
vidieť ako sú pravidlá na úrovni logického počtu zoskupené do taktík
a a tieto do metód. Pravá strana ukazuje rozvinutie vysoko-úrovňových
metód späť na úroveň pravidiel logického počtu.
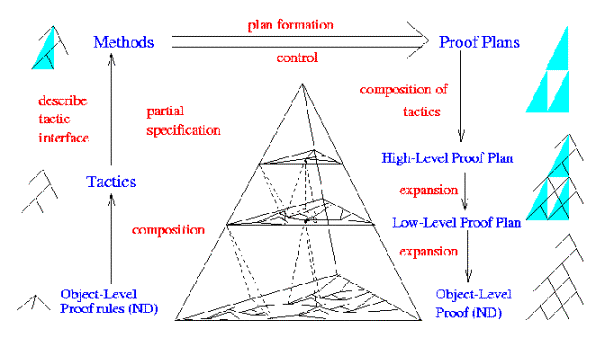
Obrázok 2.2.1 - Údajová štruktúra o pláne
dôkazu (Proof plan data structure – PDS) – prevzatá z [3]
3 Plánovanie dôkazov pomocou znalostí
Matematici zhromažďovali znalosti z riešenia matematických problémov
viac storočí. Matematik je skôr expert v úzko špecializovanej oblasti ako
univerzálny expert. To znamená expertné znalosti sú kľúčom k úspechu,
samozrejme niekoľko všeobecných techník a matematických znalostí je
potrebných tiež.
V tejto kapitole uvediem ktoré znalosti sú k dispozícii, ako ich
môžeme reprezentovať, ako môžu byť použité a ako ich architektúra
systému sprístupní pre plánovanie dôkazov.
3.1
Metódy
Základnými matematickými znalosťami sú metódy, procedúry, matematické
triky, ktoré boli a sú úspešne používané matematikmi, taktiež diagramy,
konštrukcie, obrázky a príklady. Všetky zohrávajú dôležitú úlohu
v objavovaní dôkazov. Na úspešné plánovanie dôkazov je však dôležité
zostrojenie metódy, ktorá zachytáva tieto techniky.
Ako objavujeme metódy? Jedna z heuristík získavania znalostí nielen
z matematických kníh je nasledujúca. Ak je metóda pomenovaná, je dôležitá.
Medzi pomenované matematické metódy patria: dôkaz diagonilizáciou alebo
indukciou, aplikácia dôležitých viet ako je hlavná veta lineárnej algebry, teórie
čísiel a pod.
Ako môžeme metódy reprezentovať? Metódy pozostávajú z deklaratívnych
špecifikácii, ktoré sa použijú pri plánovacom procese a z rozvojovej
funkcie, ktorá rozvíja metódu do čiastočného dôkazového plánu. Rozlišujeme
špecifikácie na objektovej a meta úrovni. Objektová úroveň zodpovedá
bežným predpokladom a efektom v plánovaní. To znamená, že určuje
dôsledky, ktoré sa zhodujú z nevyriešenými cieľmi a ktoré musí metóda
splniť (spätné plánovanie). Tiež dôsledky, ktoré sú v plánovacom stave,
keď je metóda použitá a dôsledky ktoré sa zhodujú z predpokladmi
v plánovacom stave a tie ktoré sú vytvárané ako nové predpoklady ,
keď je metóda použitá v doprednom plánovaní.
Špecifikácie na meta úrovni zachycujú pomocou meta jazyka lokálne podmienky
pre aplikáciu metódy. Vlastnosti a vzťahy ktoré musia byť splnené, aby sa
dôsledky mohli pomocou metódy spracovať.
WMEGA zobrazuje metódy ako rámcové údajové
štruktúry (Tabuľka 3.1.1).
Tabuľka 3.1.1 – Reprezentácia metódy
|
Metóda: Indukcia |
|
|
Predpoklady |
/L1, /L2 |
|
Závery |
0L3 |
|
Podmienky
použitia |
Sort(n)=Nat |
|
Dôkazová
schéma |
L1. d P(0) (baseCase) L2. d P(k) t P(k+1)
(stepCase) L3. d ¼n, P(n) (IndAxiom;L1,L2) |
Predpoklady a závery predstavujú logickú špecifikáciu. Závery by mali
logicky plynúť z predpokladov. Znaky / a 0 indikujú špecifikáciu na objektovej
úrovni, pričom 0 závery sú zmazané ako nevyriešené ciele, / predpoklady sú pridané ako nevyriešené ciele, 0 predpoklady sú zmazané predpoklady a / závery sú pridané ako predpoklady do
čiastočného plánu.
Napríklad v tabuľke 3.1.1 vidíme, že metóda má tri špecifikácie na
objektovej úrovni: /L1, /L2 a 0L3. L1 je skratka pre dôsledok
v dôkazovom riadku L1 v dôkazovej schéme. Dôsledok L3 je zmazaný ako
cieľ a dôsledky L1 a L2 sú pridané ako nové podciele.
Podmienky použitia sú formulované pomocou meta jazyka. Špecifikujú lokálne
a legálne podmienky použitia metódy. V horeuvedenom príklade
podmienkou použitia metódy je, aby n bolo prirodzené číslo.
Dôkazová schéma obsahuje informácie pre schematické rozvinutie metódy
a tým zachytáva sémantiku tejto metódy. Schematický rozvoj pridáva
čiastočný plán do PDS, ktorý je definovaný touto dôkazovou schémou. Napravo sú
vždy taktiky, metódy, alebo volania do externého systému. V prípade L1 je
to baseCase taktika, ktorá má dokázať P pre číslo 0.
3.2 Uvažovanie na meta úrovni
Napriek tomu, že metódy zapúzdrujú v sebe niekoľko dôkazov na úrovni
logického počtu, preto dôkazové plány sú všeobecne oveľa kratšie ako ich
rozvinutie na logickú úroveň, stavový priestor je stále príliš veľký. Dôvodom
je počet alternatívnych metód, ktoré sa môžu použiť v každom kroku
a hlavne, že matematické dôkazy majú potencionálny stavový priestor
nekonečný. Z tohto dôvodu sú potrebné špeciálne techniky na redukovanie
a riadenie prehľadávania v plánovaní dôkazov.
Vedomé hľadanie je výhodné v doménach, kde existujú riadiace
znalosti a matematika je práve takou oblasťou, kde tieto znalosti
sú k dispozícii. Keďže metódy reprezentujú matematicky rozumné kroky,
riadiace znalosti umožňujú skôr vyjadriť matematickú „intuíciu“ ako len
syntaktickú informáciu ako pri klasickom ATP. Problém je, že sa ťažko používajú
a primerane reprezentujú tieto znalosti.
Reprezentácia riadiacich znalostí je závislá na type znalosti, ktoré ju
predstavujú: legálne alebo heuristické znalosti, lokálne, alebo globálne
znalosti. Globálne znamená, že vyhodnocovacia procedúra musí prejsť celú PDS
a jej históriu, tiež časové zdroje, používateľský model a iné
globálne nastavenie v rámci teórie v ktorej je formulovaný problém.
Pričom legálne a lokálne znalosti sú zakódované do podmienok použitia
metódy, heuristické znalosti do riadiacich pravidiel. Tieto môžu byť
použité na uvažovanie na meta úrovni, ktoré je veľmi dôležité v matematike.
Preferuje sa explicitná a modulárna reprezentácia heuristickej
znalosty v deklaratívnych riadiacich pravidlách pred „na tvrdo“ zakódovanou
znalosťou do plánovača, alebo metódy. Toto je veľmi užitočné, lebo rovnaké
metódy sa môžu použiť v rôznych teóriách s rôznymi riadiacimi
pravidlami.
Ďalším dôvodom pre použitie riadiacich pravidiel je, že modulárne
implementované a deklaratívne reprezentované riadiace pravidlá uľahčujú
modifikáciu a rozšírenie riadiacich znalostí. Ak sú potrebné nové riadiace
informácie pre nové prípady riešenia problému, stačí modifikovať tieto pravidlá
alebo pridať ďalšie, na rozdiel od opakovanej implementácie procedurálne
napísaných riadiacich komponentov plánovača.
Tiež deklaratívna reprezentácia riadiacich pravidiel môže slúžiť ako základ
pre automatizované učenie riadiacich pravidiel, ako je to realizované
v niekoľkých systémoch.
V systéme WMEGA, riadiaca jednotka vyhodnocuje
riadiace pravidlá a riadi plánovač dôkazov v jeho voľbách medzi
niekoľkými možnosťami, podobne ako expertný systém, ktorý zužuje možnosti
výberu pravidiel. Riadiace pravidlá
majú predpoklad a dôsledok. Predpoklad určuje všeobecný kontext
v ktorom je použiteľný, jeho vyhodnotenie zaručuje jeho použitie, alebo
zavrhnutie. Dôsledok obsahuje odporúčanie na výber špecifikovanej podmnožiny
kandidátov, na zavrhnutie, alebo na preferovanie jedeného kandidáta nad druhým.
Máme nasledovné triedy riadiacich pravidiel k dispozícii
v systéme WMEGA:
-
method-choice
na výber medzi niekoľkými metódami,
-
sequent
choice na výber medzi cieľmi, alebo predpokladmi
-
strategy-choice
na výber alebo zjemnenie stratégie
Použitie riadiacich pravidiel umožňuje rozšírenie plánovacieho algoritmu
zobrazeného v tabuľke 3.2.1 (Porovnaj s tabuľkou 2.1.1)
Tabuľka 3.2.1 – Kostra riadeného spätného
plánovania
Spätne-Zjemnuj-PlánK(o,G)
Ukončenie: if cieľová agenda G prázdna, then Riešenie
if žiadny operátor sa nedá použiť, then
Neúspech
Výber cieľa: Vyhodnoť riadiace pravidlá (pre ciele)
vráť G’ pričom G’`G,
Vyber nevyriešený cieľ gcG’.
Výber operátora:
- Vyhodnoť riadiace pravidlá (pre
operátory) vráť O’`O,
- Pre každý operátor op c O’
pre každý /-efekt e z op
nech s je také, že platí es = g
if
podmienky-použitia(ops) = true,
then
op je aplikovateľné.
- Vyber jeden použiteľný M
- vlož M do o
- vlož obmedzenia do o
- obnov G.
Rekurzia: Zavolaj Spätne-Zjemnuj-PlánK na zjemnenom
čiastočnom pláne o.
3.3 Integrácia externých uvažovacích systémov
Vo väčšine matematických dôkazoch sú logické kroky kombinované
s určitým špecializovaným uvažovaním alebo efektívnym výpočtom. Napr., výpočet integrálov, riešenie rovníc
a pod. Toto špecializované uvažovanie nespolupracuje s klasickými ATP
systémami najlepšie, lebo systémy alebo algoritmy úzko špecializované dokážu
oveľa efektívnejšie pracovať. Reprezentujú objekty (reálne alebo racionálne
čísla) s ktorými tieto systémy pracujú pomocou špecializovaných údajových
typov.
V krátkosti spomeniem externé uvažovacie systémy, ktoré sú integrované
do systému WMEGA z dôrazom na tie črty, ktoré sú
dôležité z hľadiska tohto článku.
3.3.1 Klasické automatizované dokazovače viet
a rozhodovacie procedúry
Prvé systémy, ktoré boli integrované do systému WMEGA boli MKRP a OTTER.
V súčasnosti sa integrujú SPASS, PROTEIN, Bliksem, EQP a Waldmeister.
Ako náhle je zostavený abstraktný plán dôkazu, môžu v sa ňom vyskytnúť
nedostatky, ktoré môžu byť odstránené jednoduchým volaním týchto externých
systémov. A práve toto je cieľom tejto integrácie.
3.3.2 Výpočtové algebraické systémy
Na efektívny výpočet symbolických počtov, WMEGA integruje do seba niekoľko
výpočtových algebraických systémov vrátene mCAS, ktorý dokáže zjednodušiť algebraické
výrazy a vyhodnotiť výrazy v procese plánovania dôkazov.
Volanie výpočtového algebraického systému je obsiahnuté v metóde alebo
funkcii, ktorá je spustená pri vyhodnotení podmienok použitia metódy.
3.3.3 Riešitelia obmedzení
Mnoho dôkazov vyžaduje konštrukciu objektu s vlastnosťami špecializovanými
na určitú teóriu. Na riešenie tohto problému sa používa riešiteľ obmedzení,
ktorý postupne obmedzuje hodnoty, ktoré
objekt môže nadobudnúť, podobne ako v programovacej logike s obmedzeniami
(CLP).
Základné obmedzenia sú také o ktorých vieme rozhodnúť priamo, napr. (X
< a). Pri zložitých obmedzeniach nám chýba
informácia k rozhodnutiu, napr. X + Y = Z, pričom len jedna
z premenných je známa. Podmienené obmedzenia majú tvar ( if c then A1 else
A2), kde c je obmedzenie.
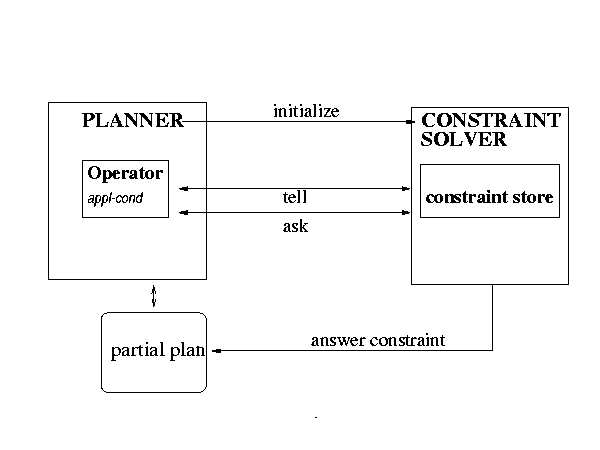
Obrázok 3.3.3.1 – Integrácia riešiteľa obmedzení
do plánovača dôkazov – prevzaté z [4]
Riešiteľ obmedzení sa integruje do plánovača dôkazov z niekoľkých dôvodov:
Je použitý v procese plánovania dôkazu, sleduje či niektorá z metód
môže byť legálne použitá, stav obmedzenia môže byť reprezentovaný obmedzením C,
ktoré ho definuje a hľadá výrazy obsahujúce kvantifikátory.
Obrázok 3.3.3.1 zobrazuje integráciu riešiteľa obmedzení do plánovača
dôkazov. Niektoré metódy, ktoré môže volať plánovač, sú prístupné pomocou
funkcie tell alebo ask. Tieto sú volané, keď sú príslušné podmienky použitia
vyhodnocované. Riešiteľ obmedzení môže vypočítať takto obmedzenie C, ktoré sa
zahrnie do čiastočného plánu.
3.4 Rozšírovanie matematických teórií
Pri plánovaní dôkazov pomocou znalostí sú matematickými znalosťami nie len
axiómy, definície, vety, ale tiež metódy, riadiace pravidlá a externé
uvažovacie systémy. Tieto znalosti sú hierarchicky organizované a uchované
v teóriách. Systém WMEGA dokáže pristupovať k týmto
základom teórií, nazývaných Mbase, ktoré obsahujú znalosti z oblasti
Základov matematiky, Teórie množín, Logického počtu a ktoré sa postupne
rozširujú na ostatné oblasti matematiky.
4 Záver
Cieľom tohto článku bolo predstaviť plánovanie dôkazov pomocou znalostí,
ktoré čerpá techniky a formalizmy z viacerých odvetví umelej
inteligencie (hierarchické plánovanie, reprezentácia znalostí
v rámcoch, explicitne reprezentované riadiace pravidlá, riešenie
obmedzení, systémy založené na prehľadávaní ako aj taktické uvažovania
a uvažovanie na meta úrovni). Použili sme všeobecný plánovač, do ktorého
sme zakódovali matematické znalosti ako metódy a riadiace pravidlá.
Riadiace pravidlá umožňujú flexibilnejšiu kontrolu a rozširujú
možnosti uvažovania na meta úrovni plánovača dôkazov. Takto deklaratívne
reprezentované riadiace znalosti vyjadrujú podmienky pre rozhodovanie sa na
základe aktuálneho stavu plánovania, plánovacej histórie, neúspešných
dôkazových pokusov, aktuálneho čiastočného plánu, stavu obmedzení, voľných
zdrojov, užívateľského modelu, teórie v ktorej sa plánuje, typického
modelu teórie, atď. Riešenie zložitejších problémov by bolo bez nich nemožné.
Na rozdiel od klasického plánovania, plánovanie dôkazov je reprezentované
matematickými teóriami, ako napr. teória grúp alebo logický počet. Tieto
obsahujú axiómy, definície, vety, lemy, ale tiež operátory, riadiace pravidlá
a externé uvažovacie systémy špecializované na určitú oblasť. Operátory
a metódy, ktoré sa volajú
reprezentujú prirodzené kroky v matematických dôkazov, pričom
riadiace pravidlá obsahujú matematické znalosti ako postupovať pri týchto
dôkazoch.
Dnešné automatizované systémy na dokazovanie viet (OTTER a SPASS) dokážu
prehľadať niekoľko miliónov klauzúl. Maximálna dĺžka dôkazu, ktoré sú schopné
nájsť sa pohybuje v rozmedziach niekoľkých stoviek dôkazových krokov.
Pomocou plánovania dôkazov sme schopný nájsť plán s niekoľkými stovkami
krokov, ktorý sa môže rozvinúť až na niekoľko tisícok dôkazových krokov na
úrovni logického počtu.
V súčasnosti sa pracuje na rozširovaní bázy znalostí
v jednotlivých oblastiach matematiky (lineárna algebra, analýza, teória
konečných množín, ...). Zhromaždenie a explicitná reprezentácia znalostí
z jednotlivých matematických oblastí bude použiteľná nielen pre počítačom
podporovanú matematiku, ale tiež pre vzdelávacie matematické systémy.
Použitá literatúra
[1] Erica
Melis, Jörg Siekmann: Knowledge-based proof planning, Artificial Intelligence 11,
pp. 65-110, 1999
[2] Christopher
Benzm·ller, et al.: WMEGA: Towards a Mathematical Assistant, CADE
1997.
[3] Proof
Planning in WMEGA.
http://www.ags.uni-sb.de/~omega/www/proof-planning.html
[4] Erica
Melis, Thobias M·ller, J·rgen Zimmer: Extensions of Constraint Solving for Proof
Planning, SEKI Report SR-99-04
Znalostné
systémy
Zimný semester 2000/2001