Zadanie č. 2

Toto zadanie sa venuje niekoľkým základným algoritmom prehľadávania stavového priestoru. Základná štruktúra algoritmu by mala byť podľa možností vyjadrená jednou funkciou.

V dokumentácii je potrebné uviesť použitý algoritmus a opísať vlastnosti tohto algoritmu - teoretické aj skutočné - koľko naozaj rozvíja uzlov. Použite aspoň dva rôzne príklady na hľadanie - vzdialenosť do cieľa napríklad 6 a 10 krokov. Porovnajte dosiahnutý výsledok pri zámene začiatočného a koncového uzla (problém 2).

Základom hodnotenia je funkčnosť programu podľa špecifikácie a dokumentácia k programu dodaná na papieri. Dokumentácia musí obsahovať:

Do systému AIS je treba odovzdať elektronickú verziu dokumentácie plus okomentované zdrojové kódy. Najlepšie zabalené do jedného zip súboru.

Ďalej sa hodnotí:

K programu je potrebné dodať sadu testovacích príkladov! Ak je program interpretovaný, môžu byť v tom istom súbore ako zdrojový kód.

Zadania a), b), c), d), e), f), g), s).

Definovanie problému 1

Úlohou je nájsť riešenie hlavolamu Bláznivá križovatka. Hlavolam je reprezentovaný mriežkou, ktorá má rozmery 6 krát 6 políčok a obsahuje niekoľko vozidiel (áut a nákladiakov) rozložených na mriežke tak, aby sa neprekrývali. Všetky vozidlá majú šírku 1 políčko, autá sú dlhé 2 a nákladiaky sú dlhé 3 políčka. V prípade, že vozidlo nie je blokované iným vozidlom alebo okrajom mriežky, môže sa posúvať dopredu alebo dozadu, nie však do strany, ani sa nemôže otáčať. V jednom kroku sa môže pohybovať len jedno vozidlo. V prípade, že je pred (za) vozidlom voľných n políčok, môže sa vozidlo pohnúť o 1 až n políčok dopredu (dozadu). Ak sú napríklad pred vozidlom voľné 3 políčka (napr. oranžové vozidlo na počiatočnej pozícii, obr. 1), to sa môže posunúť buď o 1, 2, alebo 3 políčka.

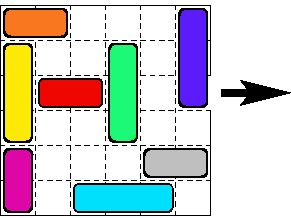
Hlavolam je vyriešený, keď je červené auto (v smere jeho jazdy) na okraji križovatky a môže z nej teda dostať von. Predpokladajte, že červené auto je vždy otočené horizontálne a smeruje doprava. Je potrebné nájsť postupnosť posunov vozidiel (nie pre všetky počiatočné pozície táto postupnosť existuje) tak, aby sa červené auto dostalo von z križovatky alebo vypísať, že úloha nemá riešenie. Príklad možnej počiatočnej a cieľovej pozície je na obr. 1.

Počiatočná pozícia Cieľová pozícia

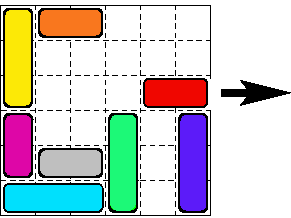Obr. 1 Počiatočná a cieľová pozícia hlavolamu Bláznivá križovatka.

Postupnosť posunov vozidiel z počiatočnej do cieľovej pozície z obr.1 je: 

VPRAVO(oranzove, 1), HORE(zlte, 1), HORE(fialove, 1), VLAVO(sive, 3),
VLAVO(svetlomodre, 2), DOLE(tmavomodre, 3), DOLE(zelene, 2), VPRAVO(cervene, 3)

Implementácia 1

Keď chceme túto úlohu riešiť algoritmami prehľadávania stavového priestoru, musíme si konkretizovať niektoré pojmy. Uvádzame príklad reprezentácie stavu, opis operátorov a cieľového stavu.

STAV

Stav predstavuje aktuálne rozloženie vozidiel. Potrebujeme si pamätať farbu každého vozidla, jeho veľkosť, pozíciu vozidla a či sa môže posúvať vertikálne alebo horizontálne. Počiatočný stav môžeme zapísať napríklad 
((cervene 2 3 2 h)(oranzove 2 1 1 h)(zlte 3 2 1 v)(fialove 2 5 1 v)
(zelene 3 2 4 v)(svetlomodre 3 6 3 h)(sive 2 5 5 h)(tmavomodre 3 1 6 v))
V tomto zápise je prvé vozidlo červené auto, ktoré sa má dostať ku bráne. Farba vozidla sa môže vynechať, ak ho konkrétna implementácia nevyžaduje. Veľkosť je vždy 2 alebo 3. Súradnice zodpovedajú ľavému hornému rohu automobilu a v tomto príklade sú súradnice počítané od ľavého horného rohu križovatky a začínajú od jednotky, prvá určuje riadok. Smer možného pohybu automobilu určuje h (horizontálny) pre pohyb vľavo a vpravo a v (vertikálny) pre pohyb hore a dole.

Vstupom algoritmov je začiatočný stav. Cieľový stav je definovaný tak, že červené auto je na najpravejšej pozícii v riadku. To vo všeobecnosti definuje celú množinu cieľových stavov a nás nezaujíma, ktorý z nich bude vo výslednom riešení.

OPERÁTORY

Operátory sú len štyri: 
(VPRAVO stav vozidlo  počet) (VLAVO stav vozidlo počet) (DOLE stav vozidlo počet) a
(HORE stav vozidlo počet)
Operátor dostane nejaký stav, farbu (poradie) vozidla a počet políčok, o ktoré sa má vozidlo posunúť. Ak je možné vozidlo s danou farbou o zadaný počet políčok posnúť, vráti nový stav. Ak operátor na vstup nie je možné použiť, výstup nie je definovaný. V konkrétnej implementácii je potrebné výstup buď vhodne dodefinovať, alebo zabrániť volaniu nepoužiteľného operátora. Všetky operátory pre tento problém majú rovnakú váhu.

Príklad použitia operátora VPRAVO, pre oranzove auto a posun o 1:

Vstupný stav: 

((cervene 2 3 2 h)(oranzove 2 1 1 h)(zlte 3 2 1 v)(fialove 2 5 1 v)
(zelene 3 2 4 v)(svetlomodre 3 6 3 h)(sive 2 5 5 h)(tmavomodre 3 1 6 v))
Výstupný stav: 
((cervene 2 3 2 h)(oranzove 2 1 2 h)(zlte 3 2 1 v)(fialove 2 5 1 v)
(zelene 3 2 4 v)(svetlomodre 3 6 3 h)(sive 2 5 5 h)(tmavomodre 3 1 6 v))

UZOL

Ako v probléme 2

ALGORITMUS

Ako v probléme 2

Definovanie problému 2

Našou úlohou je nájsť riešenie 8-hlavolamu. Hlavolam je zložený z 8 očíslovaných políčok a jedného prázdneho miesta. Políčka je možné presúvať hore, dole, vľavo alebo vpravo, ale len ak je tým smerom medzera. Je vždy daná nejaká východisková a nejaká cieľová pozícia a je potrebné nájsť postupnosť krokov, ktoré vedú z jednej pozície do druhej.

Príkladom môže byť nasledovná začiatočná a koncová pozícia:

Začiatok:
1 2 3
4 5 6
7 8  
  Koniec:
1 2 3
4 6 8
7 5  

Im zodpovedajúca postupnosť krokov je: VPRAVO, DOLE, VĽAVO, HORE.

Implementácia 2

Keď chceme túto úlohu riešiť algoritmami prehľadávania stavového priestoru, musíme si konkretizovať niektoré pojmy:

STAV

Stav predstavuje aktuálne rozloženie políčok. Počiatočný stav môžeme zapísať napríklad 
((1 2 3)(4 5 6)(7 8 m))
alebo 
(1 2 3 4 5 6 7 8 m)
Každý zápis má svoje výhody a nevýhody. Prvý (vo všeobecnosti) umožňuje spracovať ľubovoľný hlavolam rozmerov m*n, druhý má jednoduchšiu realizáciu operátorov.

Vstupom algoritmov sú práve dva stavy: začiatočný a cieľový. Vstupom programu však môže byť aj ďalšia informácia, napríklad výber heuristiky.

OPERÁTORY

Operátory sú len štyri: 
VPRAVO, DOLE, VLAVO a HORE
Operátor má jednoduchú úlohu - dostane nejaký stav a ak je to možné, vráti nový stav. Ak operátor na vstupný stav nie je možné použiť, výstup nie je definovaný. V konkrétnej implementácii je potrebné výstup buď vhodne dodefinovať, alebo zabrániť volaniu nepoužiteľného operátora. Všetky operátory pre tento problém majú rovnakú váhu.

Príklad použitia operátora DOLE:

Vstup: 

((1 2 3)(4 5 6)(7 8 m))
Výstup: 
((1 2 3)(4 5 m)(7 8 6))

HEURISTICKÁ FUNKCIA

Niektoré z algoritmov potrebujú k svojej činnosti dodatočnú informáciu o riešenom probléme, presnejšie odhad vzdialenosti od cieľového stavu. Pre náš problém ich existuje niekoľko, môžeme použiť napríklad
  1. Počet políčok, ktoré nie sú na svojom mieste
  2. Súčet vzdialeností jednotlivých políčok od ich cieľovej pozície
  3. Kombinácia predchádzajúcich odhadov
Tieto odhady majú navyše mierne odlišné vlastnosti podľa toho, či medzi políčka počítame alebo nepočítame aj medzeru.

Príklad:
Heuristika č. 2, bez medzery, odhaduje vzdialenosť nasledujúcich dvoch stavov na
1 2 3
4 5 6
7 8  
 
7 8 6
5 4 3
2   1 

4 + 3 + 1 + 1 + 1 + 1 + 2 + 2 = 15

UZOL

Stav predstavuje nejaký bod v stavovom priestore. My však od algoritmov požadujeme, aby nám ukázali cestu. Preto musíme zo stavového priestoru vytvoriť graf. Našťastie to nie je zložitá úloha. Stavy jednoducho nahradíme uzlami.

Čo obsahuje typický uzol?
Musí minimálne obsahovať

Okrem toho môže obsahovať ďalšie informácie, ako

Uzol by však nemal obsahovať údaje, ktoré sú nadbytočné a príslušný algoritmus ich nepotrebuje. Pri zložitých úlohách sa generuje veľké množstvo uzlov a každý zbytočný bajt v uzle dokáže spotrebovať množstvo pamäti a znížiť rozsah prehľadávania algoritmu. Nedostatok informácií môže zase extrémne zvýšiť časové nároky algoritmu. Použité údaje zdôvodnite.

ALGORITMUS

Každé zadanie používa svoj algoritmus, ale algoritmy majú mnohé spoločné črty. Každý z nich potrebuje udržiavať informácie o uzloch, ktoré už kompletne spracoval a o uzloch, ktoré už vygeneroval, ale zatiaľ sa nedostali na spracovanie. Algoritmy majú tendenciu generovať množstvo stavov, ktoré už boli raz vygenerované. S týmto problémom je tiež potrebné sa vhodne vysporiadať, zvlášť u algoritmov, kde rovnaký stav neznamená rovnako dobrý uzol.

Činnosť nasledujúcich algoritmov sa dá z implementačného hľadiska opísať nasledujúcimi všeobecnými krokmi:

  1. Vytvor počiatočný uzol a umiestni medzi vytvorené a zatiaľ nespracované uzly
  2. Ak neexistuje žiadny vytvorený a zatiaľ nespracovaný uzol, skonči s neúspechom - riešenie neexistuje
  3. Vyber najvhodnejší uzol z vytvorených a zatiaľ nespracovaných, označ ho aktuálny
  4. Ak tento uzol predstavuje cieľový stav, skonči s úspechom - vypíš riešenie
  5. Vytvor nasledovníkov aktuálneho uzla a zaraď ho medzi spracované uzly
  6. Vytrieď nasledovníkov a ulož ich medzi vytvorené a zatiaľ nespracované
  7. Choď na krok 2.
Uvedené kroky sú len všeobecné a pre jednotlivé algoritmy ich treba ešte vždy rôzne upravovať a optimalizovať.

Niekoľko výsledkov z prehľadávania do šírky v M*N hlavolame.

Definovanie problému 3

Eulerov kôň

Úlohou je prejsť šachovnicu legálnymi ťahmi šachového koňa tak, aby každé políčko šachovnice bolo prejdené (navštívené) práve raz. Riešenie treba navrhnúť tak, aby bolo možné problém riešiť pre štvorcové šachovnice rôznych veľkostí (minimálne od veľkosti 5 x 5 do 20 x 20) a aby cestu po šachovnici bolo možné začať na ľubovoľnom východziom políčku.

Jedno z mnohých riešení Eulerovho koňa s šachovnicou o rozmeroch 5x5 je napríklad toto:

11621107
221181520
1722569
122341914
31813245
V tomto príklade sa úspešná cesta Eulerovho koňa začala v ľavom hornom rohu (označenom číslom 1) a skončila uprostred šachovnice (na políčku označenom číslom 25), čísla označujú poradové číslo ťahu.

Príklad neúspešného riešenia Eulerovho koňa pre šachovnicu 7 x 7 (ale aj 6 x 6 a 5 x 5) je tu:
 
 
 
 8
 14
7925
1036
Po 10-tich ťahoch sa cesta koňa po šachovnici skončila (neúspechom) v políčku v ľavom dolnom rohu, keďže z tohto miesta už neexistuje žiaden legálny ťah, ktorý by bol pre Eulerovho koňa zároveň aj prípustný, t.j. viedol by na ešte nenavštívené políčko.

STAV, OPERÁTORY, ...

Sú podobné ako v probléme č.2. Nezabudnite, že kôň má vo všeobecnosti 8 možností skoku, ak nie je limitovaný okrajom šachovnice alebo už použitým miestom, čo znamená 8 operátorov.

POZNÁMKA 1

Pre problém Eulerovho kôňa treba v oboch úlohách uvažovať s tým, že pre niektoré východzie políčka a niektoré veľkosti šachovnice riešenie neexistuje. Program preto treba navrhnúť a implementovať tak, aby sa v prípade, že do určitého času, resp. počtu krokov riešenie nenájde, zastavil a signalizoval neúspešné hľadanie. Maximálny počet krokov, resp. maximálny čas hľadania by preto mal byť ako jeden zo vstupných (voliteľných) parametrov programu. Pre toto zadanie a testovacie príklady je odporúčaný maximálny počet krokov 100 tisíc, resp. maximálny čas 60 sekúnd.

Úlohy:

a)
Problém 1. Použite algoritmus prehľadávania do šírky a do hĺbky. Porovnajte ich výsledky.

b)
Problém 1. Použite algoritmus cyklicky sa prehlbujúceho hľadania.

c)
Problém 2. Použite algoritmus obojsmerného hľadania.

d)
Problém 2. Použite algoritmus lačného hľadania, porovnajte výsledky heuristík 1. a 2.

e)
Problém 2. Použite A* algoritmus, porovnajte výsledky heuristík 1. a 2.

f)
Problém 3. Algoritmom slepého prehľadávania (do hĺbky) je možné nájsť (všetky) riešenia (v bežných výpočtových – čas a pamäť – podmienkach PC) iba pri šachovniciach do veľkosti 6x6, max 7x7. Implementujte tento algoritmus pre šachovnice s rozmermi 5x5 a 6x6 a skúste nájsť prvých 5 riešení pre každú šachovnicu tak, že pre šachovnicu 5x5 aj 6x6 si vyberte náhodne 5 východzích bodov (spolu teda 10 východzích bodov) s tým, že jeden z týchto bodov je (pre každú šachovnicu) ľavý dolný roh a pre každý z týchto bodov nájdite (skúste nájsť) prvé riešenie. V prípade, že ho v stanovenom limite nenájdete, signalizujte neúspešné hľadanie. V diskusii potom analyzujte pozorované výsledky.

g)
Problém 3. b. Pre riešenie problému Eulerovho koňa existuje veľmi dobrá a pritom jednoduchá heuristika, skúste na ňu prísť sami. Ak sa vám to do týždňa nepodarí, pohľadajte na dostupných informačných zdrojoch heuristiku (z roku 1823!), prípadne konzultujte na najbližšom cvičení cvičiaceho. Implementujte túto heuristiku do algoritmu prehľadávania stromu do hĺbky a pre šachovnicu 8x8 nájdite pre 10 rôznych východzích bodov jedno (prvé) správne riešenie (pre každý východzí bod). Algoritmus s heuristikou treba navrhnúť a implementovať tak, aby bol spustiteľný aj pre šachovnice iných rozmerov než 8x8. Treba pritom zohľadniť upozornenie v Poznámke 1. Je preto odporúčané otestovať implementovaný algoritmus aj na šachovnici rozmerov 7x7, prípadne 9x9 a prípadné zistené rozdiely v úspešnosti heuristiky analyzovať a diskutovať.

s)
Voliteľný problém. Namiesto niektorého z predchodzích zadaní je možné riešiť problém Sokoban. Je náročnejší na implementáciu a riešiť je ho možné po schválení cvičiacim.

Odporúčaná literatúra:

Návrat a kol.: Umelá Inteligencia, STU Bratislava.