Algoritmy pre stromy
|
|
Vyhľadávanie extrému v strome
|
Popis |
|
Ďalším vyhľadávacím problémom v strome je nájdenie minima alebo maxima. Nehľadáme teda konkrétne nami zadaný prvok ale nejakú vlastnosť stromu. Tou je najmenší a najväčší prvok v strome.
|
Vstupy algoritmu |
|
Vstupom je strom, v ktorom chceme vyhľadávať. Podľa zvoleného algoritmu potom bude postup zodpovedať nájdeniu minima alebo maxima.
|
Princíp činnosti |
|
Ak algoritmus hľadá prvok s najmenšou (resp. najväčšou) hodnotou, vie že tento prvok sa nachádza najviac vľavo (resp. vpravo) v strome. Ak sa teda bude stále vnárať do ľavého (resp. pravého) podstromu, dostane sa až k uzlu s najmenšou (resp. najväčšou) hodnotou. Keď už vrchol nemá nasledovníka a obsahuje nulový ukazovateľ na nasledujúci ľavý (resp. pravý) podstrom, algoritmus sa končí, pretože práve toto je minimálny (resp. maximálny) prvok v strome.
|
Výstupy algoritmu |
|
Výstupom môže byť hodnota minima alebo maxima alebo ukazovateľ na uzol, ktorý uchováva túto hodnotu.
|
Vývojový diagram |
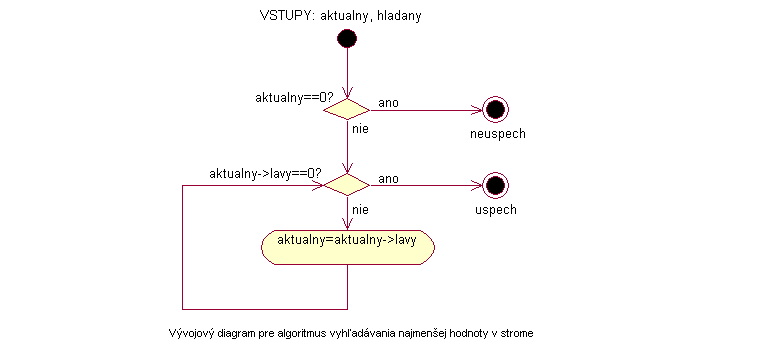 |
Implementácia |
| | //vyhladavanie minimalnej hodnoty v strome urcenom uzlom "uzol" pomocou cyklu while
//funkcia vracia ukazovatel na uzol s minimalnou hodnotou
CUzol* najdi_cykl_min_uzol(CUzol* uzol){
if (uzol)
while (uzol->lavy()) uzol=uzol->lavy();
return uzol;
} |
| Ďalšie implementácie |
Vizualizácie |
| Príklad |
|
Časová zložitosť |
|
Pri hľadaní minima alebo maxima vykoná algoritmus vždy toľko cyklov, aký hlboký je prehľadávaný strom. Pri každom kroku zisťuje, či ešte existuje (má v aktuálnom uzle nenulový ukazovateľ) nasledujúci vrchol, na ktorý by mohol prejsť. Preto pri hľadaní minima urobí (log(2) n) + 1 porovnaní. Posledné porovnanie skončí neúspechom, pretože tento uzol už nemá nasledovníka a až vtedy algoritmus vie s určitosťou povedať, že toto je hľadaný extrém.
|
| |
| Grafy, tabuľky a porovnanie s predchádzajúcimi algoritmami |
| |
| |
|

