|
|
Grafy a tabuľky |
| Vyhľadávanie extrému (maxima)
|
Priemerné počty porovnaní vybraných implementácií |
//najdenie maximalneho prvku (s najvacsou hodnotou) v poli
//funkcia vracia hodnotu maxima
template < class T, int velkost_ >
T CPole < T, velkost_ > ::najdi_sekv_hodnotu_max(){
T hodn_max=pole_[0];
int index=1;
while (++p_a_porovnani_ && index < velkost_) {
++p_a_cyklov_;
if (++p_b_porovnani_ && pole_[index] > hodn_max) hodn_max=pole_[index];
index++;
}
return hodn_max;
} |
| Počet porovnaní, cyklov a času trvania algoritmu pre úspešné vyhľadávanie. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_a_cyklov_ |
čas |
| 10 |
10,00 |
9,000 |
9,000 |
0,1314 |
| 100 |
100,0 |
99,00 |
99,00 |
0,8590 |
| 1.000 |
1000,0 |
999,0 |
999,0 |
7,771 |
| 10.000 |
10000,0 |
9999,0 |
9999,0 |
76,60 |
| 100.000 |
100000,0 |
99999,0 |
99999,0 |
918,0 |
|
Na to, aby algoritmus dokázal nájsť maximum v neusporiadanom poli, musí ho celé prejsť. Keďže prvý prvok na začiatku prehlásime za minimum, je počet cyklov rovný n-1, podobne ako počet k tomu prislúchajúcich porovnaní. Celkový počet porovnaní je vždy rádovo 2*n (presnejšie n+n-1). |
| |
| |
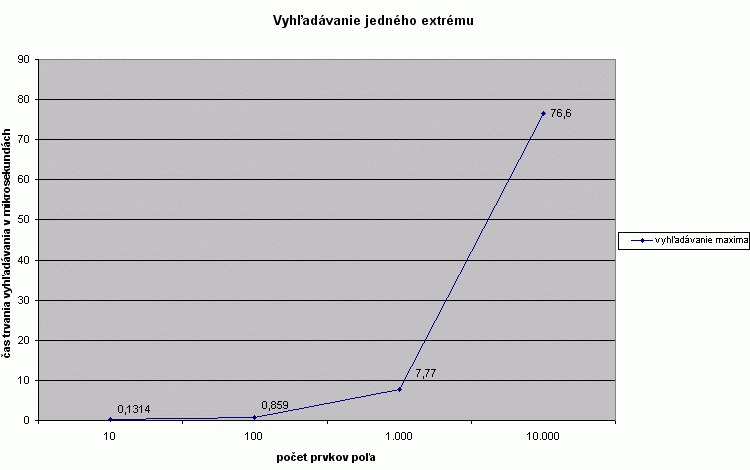
Závislost dĺžky času trvania algoritmu od veľkosti vstupného pola |
Časová závislosť dĺžky trvania algoritmu od veľkosti vstupného poľa je lineárna. Výraznejšie odchýlky môžeme pozorovať iba pre veľmi malé (rádovo 10 prvkov) a veľmi veľké (rádovo 100.000 prvkov) polia. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| vyhľadávanie maxima |
0,1314 |
0,8590 |
7,770 |
76,60 |
918,0 |
|
| |
| |
Porovnanie algoritmu s predchádzajúcimi algoritmami |
Vyhľadávanie jedného extrému je veľmi podobne časovo náročné neúspešnému sekvenčnému vyhľadávaniu. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| neúspešné sekvenčné vyhľadávanie s p=0,9 |
0,1203 |
0,7900 |
7,310 |
72,80 |
962,0 |
| vyhľadávanie jedného extrému |
0,1314 |
0,8590 |
7,770 |
76,60 |
918,0 |
|
| |
| |
| Poznámka: Algoritmy boli testované na počítači s procesorom AMD Athlon(tm) XP 1700+ a s 256 MB operačnou pamäťou pod operačným systémom Windows XP. Všetky časy uvedené v tabuľke sú v mikrosekundách. |



