|
|
Grafy a tabuľky |
| Vyhľadávanie oboch extrémov súčasne
|
Priemerné počty porovnaní vybraných implementácií |
//najdenie minimalneho a maximalneho prvku (prvok s najmensou a najvacsou hodnotou) v poli
//hodnota minima bude po ukonceni funkcie na adrese &hodn_min a
//hodnota maxima na adrese &hodn_max
template < class T, int velkost_ >
void CPole < T, velkost_ > ::najdi_sekv_hodnoty_min_max(int& hodn_min, int& hodn_max){
if (++p_b_porovnani_ && pole_[0] < pole_[1]) {
hodn_min=pole_[0];
hodn_max=pole_[1];
}
else {
hodn_min=pole_[1];
hodn_max=pole_[0];
}
int index=2;
while (++p_a_porovnani_ && index+1 < velkost_) {
++p_a_cyklov_;
if (++p_b_porovnani_ && pole_[index] < pole_[index+1]) {
if (++p_b_porovnani_ && pole_[index] < hodn_min)
hodn_min=pole_[index];
if (++p_b_porovnani_ && pole_[index+1] > hodn_max)
hodn_max=pole_[index+1];
}
else {
if (++p_b_porovnani_ && pole_[index+1] < hodn_min)
hodn_min=pole_[index+1];
if (++p_b_porovnani_ && pole_[index] > hodn_max)
hodn_max=pole_[index];
}
index+=2;
}
if (++p_a_porovnani_ && index==velkost_) return;
if (++p_b_porovnani_ && pole_[index] < hodn_min) {
hodn_min=pole_[index];
return;
}
if (++p_b_porovnani_ && pole_[index] > hodn_max) hodn_max=pole_[index];
return;
} |
| Počet porovnaní, cyklov a času trvania algoritmu pre úspešné vyhľadávanie. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_a_cyklov_ |
čas |
| 10 |
6,000 |
13,00 |
4,000 |
0,1054 |
| 100 |
51,00 |
148,0 |
49,00 |
0,9187 |
| 1.000 |
501,0 |
1498,0 |
499,0 |
8,932 |
| 10.000 |
5001,0 |
14998,0 |
4999,0 |
90,40 |
| 100.000 |
50001,0 |
149998,0 |
49999,0 |
1173,9 |
|
Algoritmus vykoná pri svojom behu vždy približne n/2 cyklov. V každom cykle najprv vykoná porovnanie či ešte v poli zostávajú nejaké prvky a potom ďalšie 3 porovnania. Celkový počet porovnaní je teda vždy rádovo 2*n. |
| |
| |
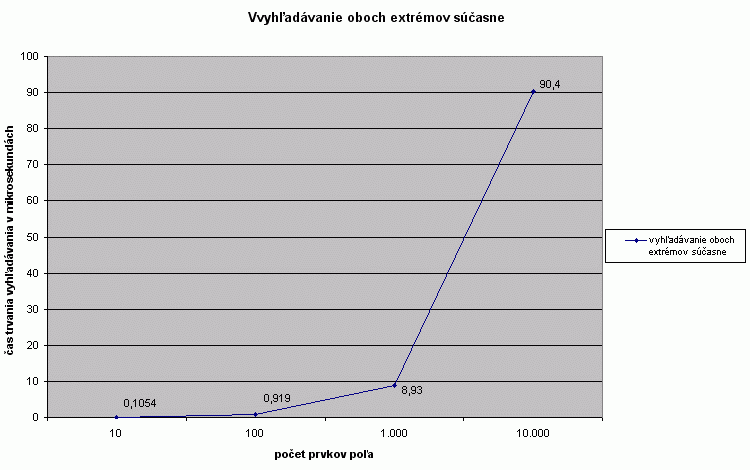
Závislost dĺžky času trvania algoritmu od veľkosti vstupného pola |
Časová závislosť dĺžky trvania algoritmu od veľkosti vstupného poľa je lineárna. Opäť môžeme pozorovať výraznejšie odchýlky iba pre veľmi malé (rádovo 10 prvkové) a veľmi veľké (rádovo 100.000 prvkové) polia. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| vyhľadávanie oboch extrémov súčasne |
0,1054 |
0,9190 |
8,930 |
90,40 |
1174,0 |
|
| |
| |
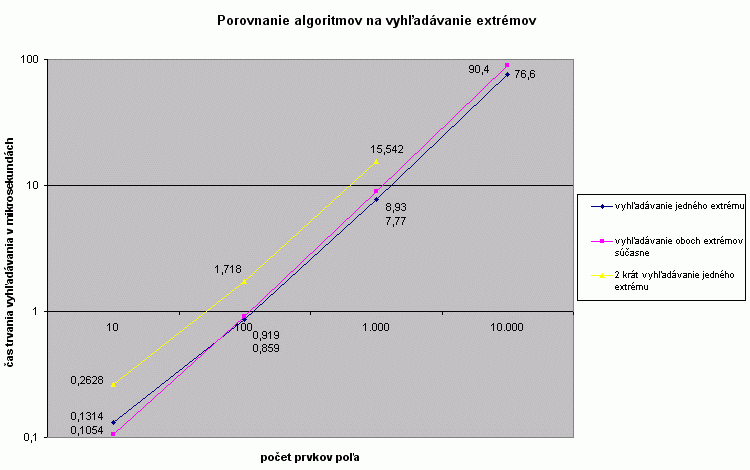
Porovnanie algoritmu s predchádzajúcimi algoritmami |
Z nameraných hodnôt vidíme, že predpoklad o približne rovnakej časovej zložitosti sa potvrdil. Oba algoritmy trvajú pre rovnaké vstupné polia približne rovnako dlho. So zväčšujúcou sa veľkosťou poľa je postupne algoritmus na vyhľadávanie oboch extrémov súčasne pomalší a rozdiel medzi porovnávanými algoritmami sa zväčšuje. Pre polia s rádovo desiatkami prvkov nastáva paradox, keď vyhľadávanie oboch extrémov súčasne je rýchlejšie ako vyhľadávanie iba jedného. Pre malé polia sa zdá byť rozhodujúci počet vykonaných cyklov, zatiaľ čo pre väčšie polia je rozhodujúca evidentne väčšia zložitosť cyklu algoritmu. V grafe môžeme vidieť aj ako dlho by približne trvalo vyhľadávanie dvoch extrémov po sebe. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| vyhľadávanie jedného extrému |
0,1314 |
0,8590 |
7,770 |
76,60 |
918,0 |
| vyhľadávanie oboch extrémov súčasne |
0,1054 |
0,9190 |
8,930 |
90,40 |
1174,0 |
| 2 krát vyhľadávanie jdného extrému |
0,2628 |
1,718 |
15,54 |
153,2 |
1836,0 |
|
| |
| |
| Poznámka: Algoritmy boli testované na počítači s procesorom AMD Athlon(tm) XP 1700+ a s 256 MB operačnou pamäťou pod operačným systémom Windows XP. Všetky časy uvedené v tabuľke sú v mikrosekundách. |



