|
|
Grafy a tabuľky |
| Vyhľadávanie k-tej hodnoty
|
Priemerné počty porovnaní vybraných implementácií |
//najdenie zadanej (k-tej najmensej) hodnoty v poli
//funkcia vracia zadanu hodnotu v poli
//(ak je v poli menej prvkov ako k, funkcia vracia maximum,
//ak je k <= 0, funkcia vracia minimum)
template < class T, int velkost_ >
T CPole < T, velkost_ > ::najdi_k_tu_hodnotu2(int k){
int lavy_o=0;
int pravy_o=velkost_-1;
int Q;
while(++p_a_porovnani_ && lavy_o!=pravy_o) {
++p_a_cyklov_;
triedenie(lavy_o, pravy_o, Q);
int M=Q-lavy_o+1;
if (++ p_a_porovnani_ && k <=M) pravy_o=Q;
else {
lavy_o=Q+1;
k=k-M;
}
}
return pole_[lavy_o];
}
//pomocna funkcia na ciastocne triedenie pola "pole"
//medzi zadanym lavym "lavy_o" a pravym "pravy_o" okrajom
//prvky s mensim indexom ako Q su po ukonceni funkcie mensie alebo rovne ako pivot
//prvky s vacsim indexom ako Q su po ukonceni funkcie vacsie alebo rovne ako pivot
//pocet prvkov mensich alebo rovnych ako pivot je ulozeny na adresu &Q
template < class T, int velkost_ >
void CPole < T, velkost_ > ::triedenie(int lavy_o, int pravy_o, int& Q){
int i=lavy_o;
int j=pravy_o;
T pivot=pole_[(lavy_o+pravy_o)/2];
do {
++p_b_cyklov_;
while (++p_b_porovnani_ && pole_[i] < pivot) i++;
while (++p_b_porovnani_ && pole_[j] > pivot) j--;
if (++p_a_porovnani_ && i <= j) {
T pomocna;
pomocna=pole_[i]; pole_[i]=pole_[j]; pole_[j]=pomocna;
i++; j--;
}
} while (++p_c_porovnani_ && i <= j);
Q=i-1;
} |
| Počet porovnaní, cyklov a času trvania algoritmu pre úspešné vyhľadávanie. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_c_porovnani_ |
p_a_cyklov_ |
p_b_cyklov_ |
čas |
| 10 |
8,000 |
20,70 |
10,00 |
3,500 |
5,000 |
0,4236 |
| 100 |
17,18 |
284,7 |
110,0 |
8,090 |
54,98 |
2,880 |
| 1.000 |
28,78 |
4321,4 |
1017,3 |
13,89 |
508,7 |
32,46 |
| 10.000 |
34,88 |
27541,0 |
10031,4 |
16,94 |
5015,7 |
276,4 |
| 100.000 |
43,73 |
245474,4 |
100106 |
21,37 |
50052,7 |
3325,8 |
|
Pri tomto algoritme už nie nie je taký dôležitý počet porovnaní ako to bolo pri predchádzajúcich algoritmoch, môžeme si však všimnúť, že sa súčet všetkých porovnaní pohybuje približne okolo hodnoty 4*n. |
| |
| |
//najdenie zadanej (k-tej najmensej) hodnoty v poli medzi lavym "lavy_o" a
//pravym "pravy_o" okrajom
//pre vyhladavanie v celom poli treba zadat lavy_o=0 a pravy_o=velkost-1
//funkcia vracia zadanu hodnotu v poli
//(ak je v poli menej prvkov ako k, funkcia vracia maximum,
//ak je k <= 0, funkcia vracia minimum)
template < class T, int velkost_ >
T CPole < T, velkost_ > ::najdi_k_tu_hodnotu(int lavy_o, int pravy_o, int k){
int M, Q;
if (++p_a_porovnani_ && lavy_o==pravy_o) return pole_[lavy_o];
else {
++p_a_cyklov_;
triedenie(lavy_o, pravy_o, Q);
M=Q-lavy_o+1;
if (++ p_a_porovnani_ && k <= M) najdi_k_tu_hodnotu(lavy_o, Q, k);
else najdi_k_tu_hodnotu(Q+1, pravy_o, k-M);
}
}
//pomocna funkcia na ciastocne triedenie pola "pole"
//medzi zadanym lavym "lavy_o" a pravym "pravy_o" okrajom
//prvky s mensim indexom ako Q su po ukonceni funkcie mensie alebo rovne ako pivot
//prvky s vacsim indexom ako Q su po ukonceni funkcie vacsie alebo rovne ako pivot
//pocet prvkov mensich alebo rovnych ako pivot je ulozeny na adresu &Q
template < class T, int velkost_ >
void CPole < T, velkost_ > ::triedenie(int lavy_o, int pravy_o, int& Q){
int i=lavy_o;
int j=pravy_o;
T pivot=pole_[(lavy_o+pravy_o)/2];
do {
++p_b_cyklov_;
while (++p_b_porovnani_ && pole_[i] < pivot) i++;
while (++p_b_porovnani_ && pole_[j] > pivot) j--;
if (++p_a_porovnani_ && i <= j) {
T pomocna;
pomocna=pole_[i]; pole_[i]=pole_[j]; pole_[j]=pomocna;
i++; j--;
}
} while (++p_c_porovnani_ && i <= j);
Q=i-1;
} |
| Počet porovnaní, cyklov a času trvania algoritmu pre úspešné vyhľadávanie. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_c_porovnani_ |
p_a_cyklov_ |
p_b_cyklov_ |
čas |
| 10 |
8,000 |
20,70 |
10,00 |
3,500 |
5,000 |
0,5477 |
| 100 |
17,18 |
284,7 |
110,0 |
8,090 |
54,98 |
3,590 |
| 1.000 |
28,78 |
4321,4 |
1017,3 |
13,89 |
508,7 |
42,26 |
| 10.000 |
34,88 |
27541,0 |
10031,4 |
16,94 |
5015,7 |
293,5 |
| 100.000 |
43,73 |
245474,4 |
100106 |
21,37 |
50052,7 |
3344,1 |
|
Počet porovnaní a cyklov sa pri zmene použitého postupu z vyhľadávania pomocou cyklu na vyhľadávanie pomocou rekurziu nemení. Súčet porovnaní je stále približne rovný 4*n. |
| |
| |
Závislost dĺžky času trvania algoritmu od veľkosti vstupného pola |
Vyhľadávanie cyklom je časovo menej náročné ako vyhľadávanie pomocou rekurzie. Pri opakovanom volaní funkcie sa totiž musia ukladať parametre volanej funkcie na zásobník. Keďže pri vyhľadávaní v cykle nepotrebujeme žiadnu réžiu navyše, je takéto vyhľadávanie rýchlejšie. Pri zväčšovaní poľa sa však spomínaný náskok postupne zmenšuje. |
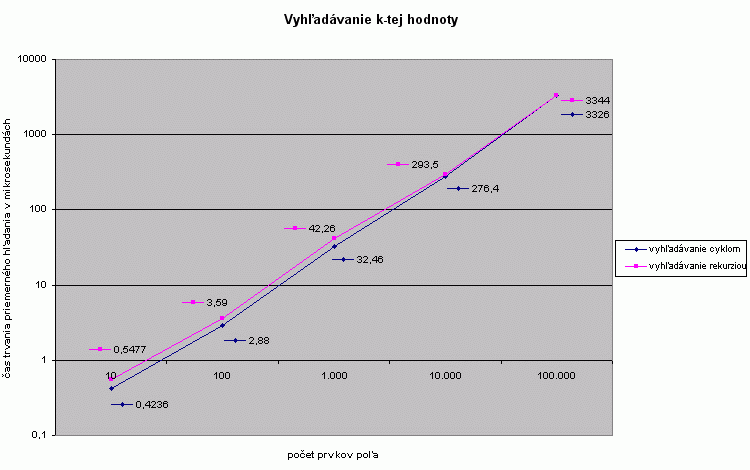 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| vyhľadávanie cyklom |
0,4236 |
2,880 |
32,50 |
276,0 |
3326,0 |
| vyhľadávanie rekurziou |
0,5477 |
3,590 |
42,26 |
293,5 |
3344,0 |
|
| |
| |
Porovnanie algoritmu s predchádzajúcimi algoritmami |
Ako bolo možné predpokladať, najnáročnejším na čas z predchádzajúcich troch algoritmov bol práve posledne opisovaný. Čas potrebný na ukončenie tohto algoritmu je približne 3 až 4 krát väčší ako čas potrebný na ostatné dva algoritmy. Bez tohto posledného by sme však nevedeli efektívne riešiť hľadanie inej ako najmenšej alebo najväčšej hodnoty v poli prvkov. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| vyhľadávanie jedného extrému |
0,1314 |
0,8590 |
7,770 |
76,60 |
918,0 |
| vyhľadávanie oboch extrémov súčasne |
0,1054 |
0,9190 |
8,930 |
90,40 |
1174,0 |
| vyhľadávanie k-tej hodnoty |
0,4236 |
2,880 |
32,46 |
276,4 |
3326 |
|
| |
| |
| Poznámka: Algoritmy boli testované na počítači s procesorom AMD Athlon(tm) XP 1700+ a s 256 MB operačnou pamäťou pod operačným systémom Windows XP. Všetky časy uvedené v tabuľke sú v mikrosekundách. |


