|
|
Grafy a tabuľky |
| Binárne vyhľadávanie
|
Priemerné počty porovnaní vybraných implementácií |
//binarne vyhladavanie zadaneho prvku "hladany" pomocou cyklu while
//pole musi byt usporiadane vzostupne (na zaciatku pola je prvok s najmensou hodnotou)
//funkcia vracia index zadaneho prvku v poli (v pripade neuspechu vyhladavania vracia -1)
template < class T, int velkost_ >
int CPole < T, velkost_ > ::najdi_bin_cykl_index(T hladany){
int lavy_o=0;
int pravy_o=velkost_-1;
while(++p_a_porovnani_ && lavy_o <= pravy_o){
++p_a_cyklov_;
int stred=(lavy_o + pravy_o)/2;
if (++p_b_porovnani_ && pole_[stred] < hladany) lavy_o=stred+1;
else if(++p_b_porovnani_ && pole_[stred] > hladany) pravy_o=stred-1;
else return stred;
}
return -1;
} |
| Počet porovnaní, cyklov a času trvania algoritmu pre úspešné vyhľadávanie. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_a_cyklov_ |
čas |
| 10 |
2,900 |
4,600 |
2,900 |
0,0739 |
| 100 |
5,800 |
8,990 |
5,800 |
0,1370 |
| 1.000 |
8,987 |
13,93 |
8,987 |
0,1742 |
| 10.000 |
12,36 |
18,82 |
12,36 |
0,2227 |
| 100.000 |
15,69 |
23,84 |
15,69 |
0,2742 |
|
Z predchádzajúcej tabuľky môžeme vidieť, že počet vykonaných cyklov už nerastie spolu s narastajúcim vstupným poľom lineárne. Ako bolo spomenuté, v priemernom úspešnom vyhľadávaní je prvok nájdený v predposlednom cykle delenia poľa na polovicu. Platí teda, že počet cyklov je približne (log(2) n)-1. Presný počet porovnaní závisí od toho v akom poradí sú zapísané v implementácii podmienky pre pokračovanie vyhľadávania v niektorej z polovíc poľa. |
| |
| Počet porovnaní, cyklov a času trvania algoritmu pre neúspešné vyhľadávanie s p=0,9. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_a_cyklov_ |
čas |
| 10 |
4,200 |
5,100 |
3,400 |
0,0999 |
| 100 |
7,560 |
9,780 |
6,600 |
0,1557 |
| 1.000 |
10,81 |
14,81 |
9,902 |
0,2061 |
| 10.000 |
14,18 |
19,74 |
13,27 |
0,2577 |
| 100.000 |
17,58 |
24,75 |
16,61 |
0,3120 |
|
Keďže pri úspešnom vyhľadávaní závisel počet cyklov algoritmu od veľkosti vstupného poľa logaritmicky, nebude tomu inak ani pri neúspešnom vyhľadávaní. Príde však k drobnej odchýlke. Zatiaľ čo pri úspešnom vyhľadávaní sa algoritmus skončil väčšinou po (log(2) n)-1 cykloch, teraz bude väčšinou potrebovať približne (log(2) n) cyklov. Musí sa totiž dostať až do najväčšej hĺbky v pomyselnom strome a až potom, keď bude ľavý okraj väčší ako pravý, skonči neúspechom. |
| |
| |
//binarne vyhladavanie zadaneho prvku "hladany" pomocou rekurzie
//pole musi byt usporiadane vzostupne (na zaciatku pola je prvok s najmensou hodnotou)
//funkcia vracia index zadaneho prvku v poli (v pripade neuspechu vyhladavania vracia -1)
template < class T, int velkost_ >
int CPole < T, velkost_ > ::najdi_bin_rek_index(int lavy_o, int pravy_o, T hladany){
if (++p_a_porovnani_ && lavy_o <= pravy_o){
++p_a_cyklov_;
int stred=(lavy_o + pravy_o)/2;
if (++p_b_porovnani_ && pole_[stred] < hladany)
return najdi_bin_rek_index(stred+1, pravy_o, hladany);
else if (++p_b_porovnani_ && pole_[stred] > hladany)
return najdi_bin_rek_index(lavy_o, stred-1, hladany);
else return stred;
}
return -1;
} |
| Počet porovnaní, cyklov a času trvania algoritmu pre úspešné vyhľadávanie. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_a_cyklov_ |
čas |
| 10 |
2,900 |
4,600 |
2,900 |
0,1424 |
| 100 |
5,800 |
8,990 |
5,800 |
0,3117 |
| 1.000 |
8,987 |
13,93 |
8,987 |
0,4800 |
| 10.000 |
12,36 |
18,82 |
12,36 |
0,6663 |
| 100.000 |
15,69 |
23,84 |
15,69 |
0,8765 |
|
Z predchádzajúcej tabuľky môžeme vidieť, že počet vykonaných cyklov už nerastie spolu s narastajúcim vstupným poľom lineárne. Ako bolo spomenuté, v priemernom úspešnom vyhľadávaní je prvok nájdený v predposlednom cykle delenia poľa na polovicu. Platí teda, že počet cyklov je približne (log(2) n)-1. Presný počet porovnaní závisí od toho v akom poradí sú zapísané v implementácii podmienky pre pokračovanie vyhľadávania v niektorej z polovíc poľa. |
| |
| Počet porovnaní, cyklov a času trvania algoritmu pre neúspešné vyhľadávanie s p=0,9. |
| počet prvkov v poli |
p_a_porovnani_ |
p_b_porovnani_ |
p_a_cyklov_ |
čas |
| 10 |
4,200 |
5,100 |
3,400 |
0,2165 |
| 100 |
7,560 |
9,780 |
6,600 |
0,3935 |
| 1.000 |
10,81 |
14,81 |
9,902 |
0,5730 |
| 10.000 |
14,18 |
19,74 |
13,27 |
0,7775 |
| 100.000 |
17,58 |
24,75 |
16,61 |
0,9949 |
|
Keďže pri úspešnom vyhľadávaní závisel počet cyklov algoritmu od veľkosti vstupného poľa logaritmicky, nebude tomu inak ani pri neúspešnom vyhľadávaní. Príde však k drobnej odchýlke. Zatiaľ čo pri úspešnom vyhľadávaní sa algoritmus skončil väčšinou po (log(2) n)-1 cykloch, teraz bude väčšinou potrebovať približne (log(2) n) cyklov. Musí sa totiž dostať až do najväčšej hĺbky v pomyselnom strome a až potom, keď bude ľavý okraj väčší ako pravý, skonči neúspechom. |
| |
| |
Závislost dĺžky času trvania algoritmu od veľkosti vstupného pola |
Dĺžka trvania vykonávania algoritmu závisí od vstupného poľa logaritmicky. Medzi priemerným úspešným a neúspešným vyhľadávaním nie sú veľké rozdiely. Vyhľadávanie v cykle je ako vidno z nameraných hodnôt vždy rýchlejšie ako vyhľadávanie pomocou rekurzie. Je to spôsobené opakovaným volaním tej istej funkcie a ukladaním parametrov funkcie na zásobník pri rekurzívnom volaní. Keďže vyhľadávanie v cykle takéto procedúry robiť nemusí, šetrí tak čas (a nielen ten). Ako je vidno, vyhľadávanie pomocou rekurzie trvá približne 2 až 3 krát dlhšie ako vyhľadávanie pomocou cyklu. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| úspešné vyhľadávanie cyklom |
0,0739 |
0,1370 |
0,1742 |
0,2227 |
0,2742 |
| neúspešné vyhľadávanie s p=0,9 cyklom |
0,0999 |
0,1557 |
0,2061 |
0,2577 |
0,3120 |
| úspešné vyhľadávanie rekurziou |
0,1424 |
0,3117 |
0,4800 |
0,6663 |
0,8765 |
| neúspešné vyhľadávanie s p=0,9 rekurziou |
0,2165 |
0,3935 |
0,5730 |
0,7775 |
0,9949 |
|
| |
| |
Porovnanie algoritmu s predchádzajúcimi algoritmami |
Zatiaľ čo pri malých poliach sú sekvenčný algoritmus s podmienkou a binárne vyhľadávanie porovnateľné, nie je tomu tak pre väčšie polia. Sekvenčné vyhľadávanie s podmienkou má totiž lineárnu zložitosť a binárne vyhľadávanie logaritmickú. Preto s rastúcou veľkosťou vstupného usporiadaného poľa sa zväčšuje aj rozdiel v efektivite. Pre pole s veľkosťou 10.000 prvkov je binárny algoritmus približne 150 krát rýchlejší ako opísaný sekvenčný algoritmus s podmienkou. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| úspešné sekvenčné s podmienkou |
0,0864 |
0,4310 |
3,890 |
38,20 |
426,0 |
| neúspešné sekvenčné s podmienkou s p=0,9 |
0,0929 |
0,4410 |
3,880 |
38,10 |
422,0 |
| úspešné binárne |
0,0739 |
0,1370 |
0,1742 |
0,2227 |
0,2742 |
| neúspešné binárne s p=0,9 |
0,0999 |
0,1557 |
0,2061 |
0,2577 |
0,3120 |
|
| |
| |
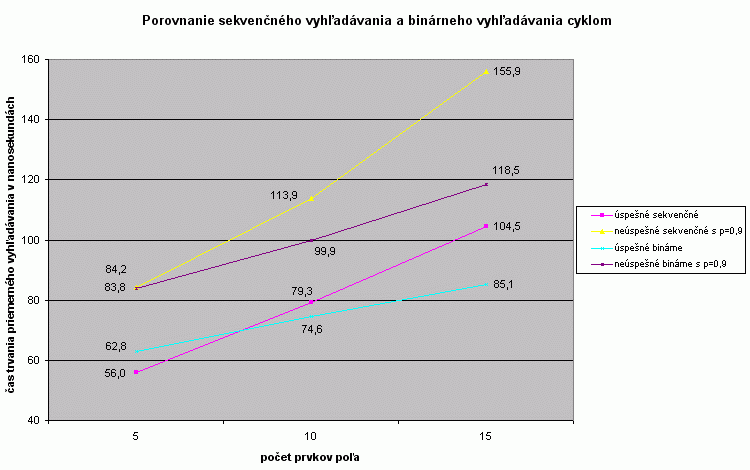
Pre malé polia (rádovo 10 prvkov) je z doteraz opísaných algoritmov najrýchlejší obyčajný sekvenčný algoritmus. Ponúka sa teda otázka, pre aké malé polia je stále binárny algoritmus tým najefektívnejším. Ako vidno z grafu, je to pre úspešné vyhľadávanie asi 8 prvkov a pre neúspešné vyhľadávanie asi 5 prvkov. Dá sa teda povedať, že pre polia obsahujúce viac ako 10 prvkov je výhodné použiť binárne vyhľadávanie. S rastúcou veľkosťou poľa rastie aj rozdiel v efektivite. |
 |
| |
5 |
10 |
15 |
| úspešné sekvenčné |
0,056 |
0,07930 |
0,1045 |
| neúspešné sekvenčné s p=0,9 |
0,0842 |
0,1139 |
0,1559 |
| binárne úspešné |
0,0628 |
0,0746 |
0,0851 |
| binárne neúspešné s p=0,9 |
0,0838 |
0,0999 |
0,1185 |
|
| |
| |
| Poznámka: Algoritmy boli testované na počítači s procesorom AMD Athlon(tm) XP 1700+ a s 256 MB operačnou pamäťou pod operačným systémom Windows XP. Všetky časy uvedené v tabuľke sú v mikrosekundách. |



