Jeden pohľad na expertné systémy tvrdí, že v podstate táto metodológia je jednoduchou alternatívou tradičného programovania. Jeden prístup navrhuje analogický postup na kontrolu správnosti expertných systémov ako sa používa v tradičnom programovaní. Napriek tomu, že tento prístup je veľmi obmedzený, je pravda, že existujú všeobecne platné pravidlá, ktoré sú aplikovateľné, tak na kontrolu správnosti tradičného spôsobu programovania, ako aj bázy znalostí. Sú to teórie štruktúrovaného programovania, ktoré sa týkajú organizácie, logiky a jednoznačnosti výrazov, či už sú to procedurálne výrazy alebo heuristické pravidlá. Tieto pravidlá slúžia na priame alebo nepriame určenie konzistencie a úplnosti v rámci bázy znalostí.
Mnohé diskusie o kontrole správnosti expertných systémov predstavovali príliš úzke chápanie tejto problematiky, bez globálneho pohľadu. V širšom ponímaní kontrola správnosti expertných systémov musí určiť nasledujúce tri oblasti:
Klúčové slová:
testovanie, opodstatnenosť, konzistentnosť, úplnosť bázy znalostí, identické,
konfliktné, obsiahnuté pravidlá, cirkularita, nadbytočnosť, úplnosť,
nedosiahnutelnosť, nereferencovatelnosť, neprípustnosť, neurčitosť, výkonnosť ES
Väčšina ľudí sa nezamyslí nad tým, či použitie daného nástroja je rozumné, praktické a efektívne. V našom prípade, ak niekto sa zaoberá vývojom expertných systémov, automaticky chce daný problém riešiť využitím expertných systémov. Neuvažuje nad použitím iných alternatívnych techník, ktoré môžu v mnohých prípadoch
rozumnejšie, praktickejšie a efektívnejšie. Takýto expertný systém , ktorý je vytvorený za každú cenu určite bude schopný dávať odpovede, avšak nikto nezaručí do akej miery možno dôverovať jeho výsledkom. Pri takomto zamýšľaní sa automaticky kladú nasledovné otázky:Predtým ako sa niekto rozhodne použiť (kúpiť, vyvíjať) expertný systém je potrebné potvrdiť opodstatnenosť použitia expertného systému a zvážiť či nejaká už existujúca alternatíva nie je praktickejšia, primeranejšia a menej nákladná.
Bohužiaľ väčšina literatúry o expertných systémoch a umelej inteligencii ani sa ani nezmieni o tejto základnej otázke. Preto akýkoľvek daný problém sa automaticky rieši vytvorením expertného systému. Vo väčšine prípadov sa ani nezvažuje použitie inej alternatívy.
Preto prvým krokom pri tvorbe expertného systému, môže to byť kompletná aplikácia alebo návrh na vývoj takéhoto systému, musí byť poskytnutie objektívneho a vyčerpávajúceho potvrdenia opodstatnenosti použitia prístupu expertného systému. Iba vtedy, ak tento prístup je obhájiteľný, môžeme pristúpiť k riešeniu menej dôležitých hľadísk tvorby.
Predtým ako sa rozhodnete vyvíjať (kúpiť) takýto systém mali by ste si položiť nasledovných päť otázok:
Ďalej by ste sa mali spýtať potencionálnych vývojárov alebo dodávateľov balíku nasledujúce otázky:
Potom čo sme si už potvrdili, že použitie expertného systému je naozaj opodstatnené a keď sme si vytvorili časť bázy znalostí, t.j. prototyp expertného systému, môžeme pristúpiť k druhej fáze. Konkrétne sa sústredíme na systematické preskúmanie logiky a integrity bázy znalostí.
Niektoré existujúce shell-y expertných systémov zahŕňajú prostriedky na čiastočnú kontrolu znalostí pri vývoji systému. Toto je typicky riešené v editori rámci znalostí a v používateľskom rozhraní shell-u. Napríklad shell EXSYS kontroluje každé pravidlo pri zadávaní na možný výskyt konfliktov medzi zadaným a už existujúcimi pravidlami v báze znalostí. Veľa shell-ov má zabudovaný prostriedok na kontrolu syntax-e, napr. na preskúšanie každého zadaného pravidla pre pravopisné chyby a
neošetrené zátvorky. Avšak veľká časť existujúcich shell-ov neposkytuje skutočne vyčerpávajúci a dôkladný prostriedok na validáciu množiny pravidiel.THERESIAS (David, 1976) bol prvý software, ktorý bol vyvinutý aby pomohol znalostným inžinierom pri validácii báz znalostí expertných systémov. Neskoršie boli vyvinuté ďalšie kontrolné balíky na podporu expertných systémov ako sú ONCOCIN, TIMM a KES.
V polovici osemdesiatych rokoch Nguyen, Perkins, Laffey a Pecora (1985,1987) ohlásili vývoj oveľa lepšieho programu CHECK. CHECK pracuje s bázami znalostí, ktoré obsahujú ak dopredné a spätné zreťazenie, konkrétne s LES (Lockheed Expert System), ktorý je programovým balíkom na vývoj expertných systémov. Tento systém sa zaoberá problémami
nekonzistentnosti a úplnosti pravidiel.Nguyen vyhlásil: "Problémy bázy znalostí môžu byť odhalené len ak syntax pravidiel je dosť obmedzená aby umožnil preskúmať dve pravidlá a určiť či existujú situácie, v ktorých obidve uspejú, alebo či výsledky použitých pravidiel sú tie isté, konfliktné alebo nezávislé." Ak je použitý neobmedzená syntax, potom v ďalšom popísané metódy vo väčšine prípadov nemôžu byť použité.
Predpokladá sa, že pravidlá sú zoskupené podľa subjektu. V prípade spätného alebo cieľom riadeného odvodzovaniab môže byť množina pravidiel pre každý cieľ nezávisle kontrolovaná. Táto podmienka však nie prísna, ale určite zjednoduší kontrolu pravidiel. Kontrola pravidiel je ešte jednoduchšia ak v predpo
klade pravidla sa objavujú iba konjunktívne klauzuly a ak v dôsledku pravidla sa objaví iba jednoduchá klauzula.Na záver by sme mali predpokladať, že odvodzovanie všetkých pravidiel je typu spätné zreťazenie a množina pravidiel je deterministická (neuvažuje sa dôveryhodnosť).
V podstate existuje päť druhov nekonzistencií, ktoré môžu byť identifikované:
Definícia:
{ P(k)} je množina predpokladov pre pravidlo k
{ C(k)} je množina dôsledkov pre pravidlo k
p(k) je jeden predpoklad z množiny { P(k)}
c(k) je jeden dôsledok z množiny { C(k)}
{ S} ={ T} znamená, že množina S sa rovná množine T
Uvažujme s nasledujúcimi dvomi pravidlami. Všimnite si, že pravidlo 1 sa stáva nadbytočným v dôsledku pravidla 2. To znamená, že obidve pravidlá sú vyhodnotené pri rovnakej množine predpokladov, kým množina dôsledkov pravidla 1 je podmnožinou množiny dôsledkov pravidla 2.
Pravidlo 1:
If A = X And B = Y
Then C = Z
Pravidlo 2:
if B = Y and A = X
Then C = Z And D = W
Definícia: pravidlo r je nadbytočné s ohľadom na pravidlo s ak
{ P(r)} = { P(s)}
a { C(r)} je podmnožinou { C(s)}
Následne môžeme pravidlo r odstrániť z množiny pravidiel.
Uvažujme s nasledujúcimi dvomi pravidlami. Tieto pravidlá sú konfliktné ak pre tú istú množinu predpokladov sú dosiahnuté iné dôsledky . V prvom prípad C = Z, kým v druhom C = W.
Pravidlo 1:
If A = X And B = Y
Then C = Z
Pravidlo 2:
If A = X And B = Y
Then C = W
Definícia: pravidlo r je v konflikte s pravidlom s ak
{ P(r)} = { P(s)}
a { C(r)} je v rozpore s { C(s)}
Ak dve pravidlá sú konfliktné, to znamená, že buď jedno alebo druhé bolo chybne formulované. Avšak môžu nastať situácie, ak pravidlá sú konfliktné a sú pritom aj korektne formulované. Uvažujme s nasledujúcim príkladom:
Pravidlo 1:
If červené vyrážky And má teplotu
Then pacient je alergický na liek A
Pravidlo 2:
If červené vyrážky And má teplotu
Then pacient je alergický na liek B
To znamená, že obidva lieky môžu vyvolať rovnaké symptómy u pacienta. Takýto výsledok najpravdepodobnejšie znamená, že sme nezadali dostatočný počet symptómov na rozlíšenie dvoch typov alergických reakcií. Avšak môže sa stať, že pacient je alergický na obidva lieky. A tak by
bolo vhodné použiť viacero hodnôt pre vyjadrenie dôsledku. Znalostní inžinieri musia určiť prípad, ktorý je pravdepodobnejší a v prípade potreby podľa toho upraviť bázu znalostí.Jedno pravidlo je obsiahnuté v druhom pravidle, ak obidve pravidlá majú rovnaké dôsledky, ale prvý obsahuje dodatočné (nepotrebné) predpoklady. V nasledujúcom prípade pravidlo 1 je obsiahnuté v pravidle 2.
Pravidlo 1:
If A = X And B = Y
Then C = Z
Pravidlo 2:
If A = X
Then C = Z
Definícia: pravidlo r je podradené pravidlu s ak
{ C(r)} = { C(s)}
a { P(s)} je podmnožinou { P(r)}
potom pravidlo r sa odstráni z bázy znalostí.
Uvažuje s nasledovnými pravidlami. Všimnite si, že ten istý dôsledok je dosiahnutý bez ohľadu na hodnotu atribútu B. A tak predpoklad obsahujúci B je nadbytočný a môže byť odstránený na vytvorenie efektívnejšieho pravidla. Pravidlá 1 a 2 majú byť nahradené jediným pravidlom: If A = X THEN C = Z
Pravidlo 1:
If A = X And B = Y
Then C = Z
Pravidlo 2:
If A = X And B = NOT Y
Then C = Z
Definícia: pravidlo r a s majú nadbytočný predpoklad v klauzule if ak:
{ C(r)} = { C(s)}
a niektorý p(r) je v konflikte s p(s)
a ostatné predpoklady sú ekvivalentné.
E. Cirkularita v reťazi inferencie
Množina pravidiel je v cirkularite, ak zreťazenie týchto pravidiel vedie k slučke alebo cyklu. Uvažujme príklad nasledujúcich troch pravidiel. V týchto pravidlách predpokladajme nasledovný cieľ:
decision. Takže, použitím spätného zreťazenia, najskôr použijeme pravidlo 2, jediné pravidlo obsahujúce decision v dôsledku. Prvý predpoklad pravidla 2 sa nachádza v dôsledku pravidla 1. Takže zreťazíme teraz pravidlo 2 s pravidlom 1. Predpoklad pravidla 1 sa nachádza v dôsledku pravidla 3, pokračujeme použitím pravidla 3. V pravidle 3 je uvedený predpoklad decision = yes. Decision sa zase vyskytuje v dôsledku pravidla 2 - koniec prvého cyklu.Pravidlo 1 (R1):
If A = X
Then B = Y
Pravidlo 2 (R2):
If B = Y And C = Z
Then decision = yes
Pravidlo 3 (R3):
If decision = yes
Then A = X
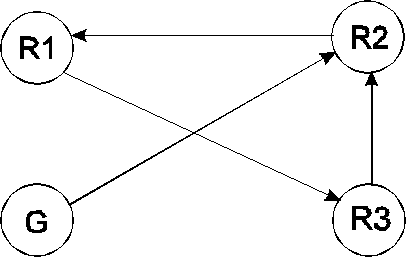
Efektívnym nástrojom na zistenie cirkularity v reťazi inferencie je použitie grafu závislosti pravidiel.
Kroky na vytvorenie grafu závislosti pravidiel:
1. Pre každé pravidlo a cieľ vytvor uzol
2. Prepoj hranou dva uzly, ak
- jeden alebo viacej predpokladov v jednom pravidle sa nachádza v jednom alebo viacerých dôsledkoch iného pravidla (hrana je orientovaná z prvého do druhého pravidla)
- cieľ sa nachádza v jednom alebo viacerých dôsledkoch nejakého pravidla ( hrana je orientovaná od cieľa smerom k pravidlu)

Postupným aplikovaním krokov 1 až 2. R1 je spojené s R3, R2 je spojené s R1, R3 je spojené s R2 a cieľ G je spojený s R2. Slučku tvoria uzly R1, R2 a R3. Slučka sa vytvorí cestou R2-R1-R3-R2. Ak vznikne slučka v grafe závislosti pravidiel, potom tým je určená aj cirkularita v reťazi inferencie množín pravidiel. Takáto cirkularita môže spôsobiť nekonečný cyklus v čase behu programu. Je samozrejmé, že by mala byť odstránená.
Existuje päť typov úplnosti v báze znalostí:
A. Nereferencované hodnoty atribútov
Uvažujme bázu znalostí, ktorá radí pri riadení investícií firmy. Jedným uvažovaným atribútom nech je úroková sadzba. Nech možné hodnoty úrokovej sadzby sú: vysoká, stredná a nízka. Ak sa aspoň jedna z týchto hodnôt neobjaví v nejakom predpoklade, potom nastane situácia nereferencovaného atribútu. Nasledujúce dve pravidlá ukazujú túto situáciu.
R1:
If úroková sadzba je vysoká
Then investuj do cenných papierov
R2:
If úroková sadzba je nízka
Then investuj do zásob
Z tohto dôvodu by mal byť validačný systém schopný signalizovať znalostnému inžinierovi, ak sa nejaká hodnota atribútu neobjaví v žiadnej podmienke množiny pravidiel. Táto kontrola môže byť dosiahnutá použitím matice, v ktorej riadky znamenajú hodnoty atribútu a stĺpce znamenajú podmienky v pravidlách. Hviezdičkou (*) označíme priesečník každého stĺpca a riadku, ak podmienka v stĺpci obsahuje hodnotu atri
bútu v riadku. Ak celý riadok v takejto matici je prázdny, to znamená, že zodpovedajúca hodnota atribútu nie je referencovaná. To znamená, že chýba buď pravidlo, alebo podmienka, alebo hodnota atribútu má byť odstránená z množiny prípustných hodnôt atribútu.| Úroková sadzba | R1 |
R2 |
| Nízka | * |
|
| Stredná | ||
| Vysoká | * |
B. Neprípustné hodnoty atribútov
Uvažujme ten istý problém o investovaní. Máme zadefinované dva atribúty: úroková sadzba a inflácia. Prípustné hodnoty úrokovej sadzby sú: nízka, stredná, vysoká. Prípustné hodnoty inflácie sú: vysoká a nízka. Ďalej uvažujme nasledovné pravidlo:
Pravidlo:
If úroková sadzba je veľmi vysoká
Or inflácia je V
Then investuj do zlatých zásob
Hodnoty veľmi vysoká pre úrokovú sadzbu a V pre infláciu, nie sú zahrnuté v množine prípustných hodnôt atribútov. Pravidlo musí byť opravené. Takéto neprípustné hodnoty môžu byť odhalené porovnaním všetkých prípustných hodnôt atribútu s hodnotami uvedenými v pravidlách. Ak neexistuje zhoda, potom nastal prípad neprípustnej hodnoty
atribútu.C. Nedosiahnuteľné okamžité dôsledky
Uvažujme uvedené pravidlo:
Pravidlo:
If A = X
Then R = W
Okamžitý dôsledok je nedosiahnuteľný v prípade ak dôsledok sa nenachádza v žiadnej podmienke nejakého pravidla. Predpokladáme hľadanie okamžitého dôsledku, čiže ďalšieho kroku v procese inferencie a nie hľadanie konečného cieľa.
D. Nedosiahnuteľné konečné dôsledky (cieľ)
Cieľ je označený ako nedosiahnuteľný (nesplniteľný) ak:
Uvažujme nasledujúce pravidlá:
R1:
If A = U
Then C = W
R2:
If C = W
Then D = X
R3:
If E = Q
Then goal = yes
Ak toto je úplná množina pravidiel, a neexistuje dotaz na zadanie hodnoty atribútu E, cieľ v pravidle 3 nie je dosiahnuteľný, lebo hodnota E sa nedá odvodiť zo žiadneho z uvedených pravidiel.
E. Nedosiahnuteľné predpoklady
Predpoklad (podmienka) pravidla je nedosiahnuteľný ak:
Pozri pravidlo 3 predchádzajúceho príkladu.
Matica závislosti pravidielMôžeme využiť maticu závislosti pravidiel na zistenie posledných troch druhov neúplnosti. Uvažujme nasledovne uvedenú bázu znalostí. Nech atribút C je asociovaný s nejakým dotazom.
Uvažujme nasledujúce pravidlá:
R1:
If A = X
Then B = Y
R2:
If C = W
Then A = X
R3:
If E = Q
Then goal = yes
Matica závislostí pravidiel je nasledovná:
Dôsledky |
||||
| Podmienky | R1 |
R2 |
R3 |
Dotaz |
| R1 | *# |
|||
| R2 | * |
|||
| R3 | G |
|||
Stĺpce matice určujú dôsledky pravidiel, kým riadky matice určujú podmienky pravidiel.
Pravidlá pre určenie úplnosti sú takéto:
Po použití týchto pravidiel, z uvedenej tabuľky môžeme vyvodiť
nasledovné:
Množina dopredne zreťazených pravidiel, alebo pravidiel riadených údajmi môže
byť kontrolovaná podobným spôsobom ako je popísané pri spätnom zreťazení. Jediný
rozdiel je v kontrole nedosiahnuteľných okamžitých dôsledkov, nedosiahnuteľných
konečných dôsledkov (cieľ), nedosiahnuteľných
Validácia pri doprednom zreťazení
Faktory dôveryhodnosti slúžia na skomplikovanie procesu va
lidácie expertných systémov. Program CHECK od Nguyen a spol., pracuje s faktormi dôveryhodnosti vo formáte známeho z MYCIN-u.A. Identické pravidlá s využitím neurčitosti
Mechanizmus určenia identických pravidiel je totožný s už uvedením bez uvažovania neurčitosti. Identické pravidlá, ktoré ostávajú v báze znalostí môžu spôsobiť vážne problémy ak sú použité faktory dôveryhodnosti, z dôvodu že ktorékoľvek pravidlo môže byť použité, čo spôsobuje viacnásobné chybné spočítanie tej istej informácie, ktorá pot
om chybne zvyšuje konečnú váhu danú všetkými asociovanými dôsledkami.B. Konfliktné pravidlá s využitím neurčitosti
Kontrola týchto chýb prebieha takisto ako bez použitia neurčitosti. Avšak, veľmi často nič nie je zle zadané ak sú použité faktory dôveryhodnosti. Pri každom dôsledku je udaná jeho dôveryhodnosť, teda pravdepodobnosť výskytu daného riešenia. Rozhodnutie je na znalostnom inžinierovi, či nechá pravidlá v pôvodnom tvare alebo ich dôsledky skombinuje použitím operátora AND.
C. Podradené pravidlá s využitím neurčitosti
Pri takomto prípade nie vždy je potrebné odstrániť pravidlo z bázy znalostí. Je možné vytvoriť pravidlá takým spôsobom, že sa dôsledku viacej obmedzeného pravidla priradí väčšia váha ako druhému pravidlu.
Pravidlo 1:
If A = X And B = Y
Then C = Z (cf = 0.7)
Pravidlo 2:
If A = X
Then C = Z (cf = 0.6)
D. Nadbytočné podmienky s využitím neurčitosti
Nadbytočné podmienky sú dôležité ak v dôveryhodnosť dvoch pravidiel je rozdielna. Ak aj dôveryhodnosť predpokladu je iná, tak potom konečná dôveryhodnosť môže byť v značnej miere rozdielna.
Pravidlo 1:
If A = X (cf11)
And B = Y (cf12)
Then C = Z (cf1)
Pravidlo 2:
If A = X (cf11)
And B = NOT Y (cf21)
Then C = Z (cf2)
E. Cirkularita v reťazi inferencie s využitím neurčitosti
Cirkularita sa dá zistiť takým istým spôsobom ako bez použitia neurčitosti. Všimnite si že slučka môže byť prerušená ak dôveryhodnosť je menšia prahová hodnota.
F. Nereferencované hodnoty atribútov a neprípustné hodnoty atribútov s využitím neurčitosti
Ošetrenie a určenie týchto chýb je identické s prípadom bez použitia neurčitosti.
G. Nedosiahnuteľné okamžité dôsledky s využitím neurčitosti
V tomto prípade detekcia nedosiahnuteľných okamžitých dôsledkov je oveľa komplexnejšia ako bez použitia neurčitosti. Okamžitý dôsledok môže byť nedosiahnuteľný aj vtedy, ak predpoklad sa nachádza v dôsledku iného pravidla.
Pravidlo 1:
If A = X (cf11=0.3)
Then D = W (cf1 = 0.6)
Pravidlo 2:
If D = W (cf21)
Then R = Z (cf2)
Ak chceme potvrdiť cieľ R = Z, musíme najprv potvrdiť podmienku D=W v 2. pravidle. D=W sa nachádza v dôsledku 1. pravidla, preto použijeme toto pravidlo. Ak atribút A je zadaný používateľom potom faktor dôveryhodnosti pre pravidlo 1 = 0.6 * 0.3 = 0.18. Ak prahová hodnota je
0.2, potom sme neuspeli pri odvodzovaní.H. Nedosiahnuteľné konečné dôsledky (cieľ) a nedosiahnuteľné predpoklady s využitím neurčitosti
Detekcia nedosiahnuteľných cieľov a predpokladov je tiež veľmi komplikovanou úlohou. Nedosiahnuteľný cieľ môže nastať aj v takom prípade, že predpoklad sa nachádza v dôsledku iného pravidla, ale toto pravidlo má dôveryhodnosť pod prahovou hodnotou.
R1:
If A = X
Then B = Y (cf)
R2:7
If B = Y
Then goal = yes (cf)
Posledným uvažovaným hľadiskom pri validácii expertného systému je overenie celkovej výkonnosti expertného systému. Je to vlastne overenie toho, ako dobre sa hodí tento systém na riešenie problémov v praxi.
Primárne kroky pri overení sú nasledovné:
Aká je presná určená úloha expertného systému ?
Úloha expertného systému by mala byť samozrejme určený už predtým ako sme sa ho odhodlali vyvíjať. Expertný systém poskytuje expertovi rady na nejakom špecifikom poli nasadenia systému. Úlohou je zdokumentovať presné ciele a požiadavky na daný systém.
Kritériá výkonnosti
Ak úloha expertného systému je už zdokumentovaná
, potom určenie kritérií, ktorými sa daný expertný systém bude posudzovať je značne ľahšou úlohou. Zavedie expertného systému má vplyv na nasledujúce oblastia: produktivita, organizácia a personál. Tieto dopady do týchto oblastí sa dajú ďalej deliť takto:Zber údajov
Jedným spôsobom zberu údajov je získať údaje z minulého obdobia v organizácii. S týmito údajmi sa potom testuje expertný systém. Kontroluje sa správnosť výsledkov. Druhou alternatívou je testovanie s množinou skúšobných prípadov (pripraví ich expert, ktorý navrhol aj bázu znalostí). Treťou alternatívou je spustenie paralelne existujúceho systému a expertného systému a porovnanie ich výsledkov.
Vyhodnotenie údajov
Typické, ale zďaleka nie perfektné vyhodnotenie výkonnosti systému je použitie metodiky zvanej cost-benefit (zefektívnenie nákladov). Podmienka takejto metodiky je ten, že je nutné nejakým spôsobom skombinovať rôzne mierky (kritériá) výkonnosti do jednej jednotky merania výkonnosti.
Zápory takéhoto prístupu sú:
1. Tento základný predpoklad je beznádejne idealistický (t.j. že sa nájde spoločná jednotka merania výkonnosti)
2. Viacero mierok výkonnosti sa nedá spolu skombinovať (napríklad ohodnotenie ľudského života v dolároch)
3. Kombinácia množstva rôznych mierok, z ktorých každá je zaťažená nejakou chybou, spôsobí agregáciu chýb vo výslednej agregovanej mierke.
Ignizio. An Introduction To Expert System - Chapter 8 - Validation.
Znalostné systémy
Zimný semester 1998/99