 |
Algoritmy usporadúvania |
Radix sort |
| Hlavné menu | Predchádzajúci | |
| Implementácia | ||
| Vizualizácia-náhodný vstup | ||
| Vizualizácia-náhodný vstup | ||
| Štatistika algoritmu |
Základné vlastnosti |
| Radix sort bol používaný najmä pri usporadúvaní diernych štítkov, dnes už je takmer nepoužívaný. [8] Metóda Radix sort je určená na usporadúvanie postupnosti prvkov. Radix sort patrí medzi najrýchlejšie algoritmy usporadúvania, avšak vo všeobecnosti nie je rýchlejší než Quick sort. Radix sort je najčastejšie používaný pri usporadúvaní desiatkových čísel, avšak môžeme použiť ľubovolný základ pre usporadúvané čísla. [3] Operačná zložitosť algoritmu je O(n*log2n). Radix sort je nekomparačný algoritmus. |
Popis |
| V algoritme Radix sort jednotlivé členy vstupnej neusporiadanej postupnosti triedime do skupín. Skupina predstavuje postupnosť prvkov, ktoré majú rovnakú hodnotu i-teho rádu, kde i+1 je krok vykonávania algoritmu. V prvom kroku je príslušnosť do skupiny určená najnižším, teda nultým rádom radených prvkov. Postupne radíme prvky do skupín podľa vyšších rádov až po posledný rád. Počet krokov algoritmu závisí od rádu prvku s najvyšším rádom. Vstupom pre prvý krok triedenia je usporadúvaná postupnosť, pre triedenia do skupín v ďalších krokoch je vstupom postupnosť, ktorá vznikne spojením čiastkových postupností z jednotlivých skupín v predchádzajúcom kroku, pričom spájanie začíname od nultej skupiny. Uvedený spôsob usporiada prvky vstupnej postupnosti vzostupne, zmenou poradia spájania skupín do postupností, ktoré sú vstupom pre nasledujúce triedenie, môžeme docieliť zostupné usporiadanie. |
Vývojový diagram |
| Na nasledujúcom obrázku je znázornený vývojový diagram pre algoritmus Radix sort, ktorý názorne popisuje spracovanie a usporadúvanie postupnosti týmto algoritmom. Uvedený diagram znázorňuje usporadúvanie postupnosti vzostupne. |
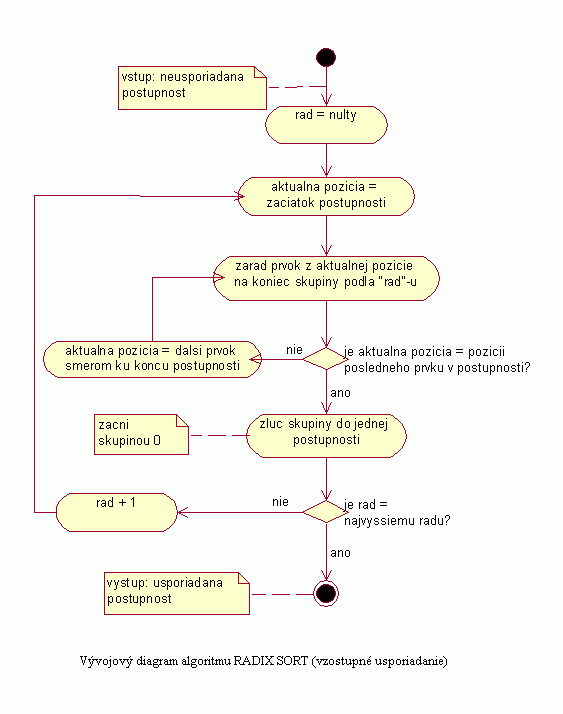 |
Výhody a nevýhody |
| Pri usporadúvaní algoritmom Radix sort je výhodné, ak usporadúvame podľa relatívne krátkeho kľúča. Napríklad kľúč typu meno+priezvisko nie je pri algoritme Radix sort výhodou. Radix sort je najvýhodnejšie použiť pri usporadúvaní veľkých postupností, avšak s krátkym kľúčom, podľa ktorého prvky usporadúvame. [3] Problémy nastávajú takisto pri usporadúvaní záporných čísel. Tento problém sa však dá riešiť. |
Zložitosť |
| Myšlienka algoritmu Radix sort spočíva v rozdeľovaní do tried, ktoré prebieha so zložitosťou O(n) v každom ráde. To znamená, že celková zložitosť algoritmu je O(L*n) , kde L je dĺžka radených prvkov. Keby sme L považovali za konštantu, operačná zložitosť Radix sort by bola O(n) . [1] Ak by bolo možné, aby L narastalo spolu s n, potom L = log n a dostaneme : |
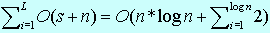 |
= O(n*log n + 2*log n) =O(n*log n) kde s je počet skupín. Zložitosť Radix sort je teda O(n) = O(n*log n) . [6] |
| Hlavné menu | Predchádzajúci | |
| Implementácia | ||
| Vizualizácia-náhodný vstup | ||
| Vizualizácia-náhodný vstup | ||
| Štatistika algoritmu |