 |
Algoritmy usporadúvania |
Merge sort |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |
Základné vlastnosti |
| Merge sort je algoritmus určený na usporadúvanie postupnosti prvkov zlučovaním. Operačná zložitosť algoritmu je O(n*log2n). Pri tejto metóde dochádza k porovnávaniu prvkov, preto Merge sort patrí medzi komparačné algoritmy. Algoritmus Merge sort je univerzálny a je možné pomocou neho zoraďovať celé i reálne čísla a aj reťazce. Merge sort je rekurzívny algoritmus, avšak je možné vytvoriť i nerekurzívnu formu so zachovaním základnej filozofie algoritmu. |
Popis |
| Algoritmus Merge Sort je založený na zlučovaní dvoch už usporiadaných postupností. Vstupnú neusporiadanú postupnosť rozdelíme na dve, po usporiadaní týchto dvoch postupností ich zlúčime a dostaneme výslednú usporiadanú postupnosť. Vstupom pre algoritmus sú dve usporiadané polia a a b (postupnosti) a výstupom usporiadané pole c, ktoré vzniklo zlúčením (merge) oboch vstupných polí. Pri vykonávaní algoritmu sú použité tri ukazovatele (a_ptr, b_ptr, c_ptr), a to ukazovatele na aktuálnu pozíciu v každom poli. Porovnáme prvky a[a_ptr] a b[b_ptr] , menší z nich je umiestnený do postupnosti c na pozíciu c[c_ptr] . Po presunutí sú dané dva ukazovatele (a_ptr alebo b_ptr a c_ptr) posunuté o jednu pozíciu. Akonáhle je jedna zo vstupných postupností prázdna (celá presunutá do výstupnej postupnosti), je zvyšok druhej postupnosti presunutý do výstupnej bezo zmeny poradia prvkov. Uvedený spôsob zoraďuje postupnosť vzostupne. Zmenou podmienky pri porovnávaní prvkov docielime zostupné usporiadanie. |
Vývojový diagram |
| Na nasledujúcom obrázku je znázornený vývojový diagram pre algoritmus Merge sort, ktorý popisuje spracovanie a usporadúvanie postupnosti týmto algoritmom. Spôsob vykonávania operácie zluc L a R je popísaný v Popise tohto algoritmu. |
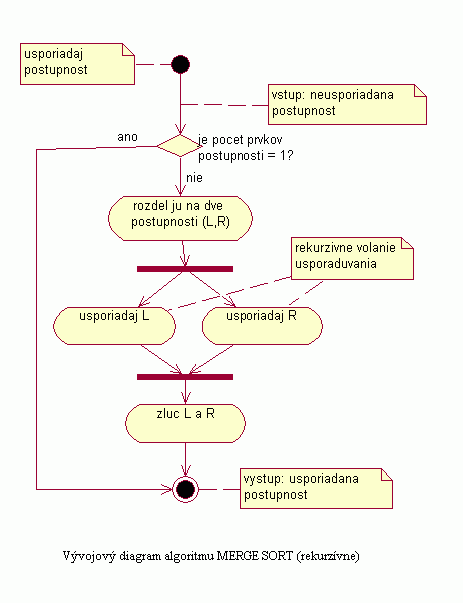 |
Výhody a nevýhody |
| Nevýhodou rekurzívneho algoritmu je, že po zlúčení dvoch čiastkových postupností je potrebné presunúť zlúčenú postupnosť na miesto zdrojových zlučovaných postupností, čo nám zaberie istý čas pri vykonávaní algoritmu. [2] Keďže Merge sort pracuje pri usporadúvaní s tromi poľami, je tento algoritmus náročný na pamäť. Keďže spracovanie reťazcov je samo o sebe pamäťovo náročné, je Merge sort nevhodný na usporadúvanie postupnosti reťazcov. Pamäťovú náročnosť zvyšuje i rekurzívnosť tohto algoritmu. Merge sort je základná metóda pre usporadúvanie sekvenčných súborov. [1] |
Zložitosť |
| Najlepšia, priemerná a najhoršia časová zložitosť sú pri algoritme Merge sort rovnaké a to O(n*log2n) . [4] Vyjadrime operačnú zložitosť algoritmu ako počet porovnaní pri zlučovaní dvoch postupností do postupnosti s n prvkami. Najlepší prípad: príklad : postupnosť I. : 1 2 3 4 postupnosť II. : 5 6 7 8 Počet porovnaní v najlepšom prípade je C(n) = n/2. Najhorší prípad: príklad : postupnosť I. : 1 3 5 7 postupnosť II. : 2 4 6 8 Počet porovnaní v najhoršom prípade je C(n) = n-1. Zložitosť usporadúvania postupnosti n prvkov O(n) sa pri algoritme Merge sort rozdelí na zložitosti usporadúvania postupnosti n/2 prvkov O(n/2) . Tak dostávame O(n) = 2* O(n/2) + C(n) . Pre najlepší prípad O(n) = 2* O(n/2) + n/2, pre najhorší prípad O(n) = 2* O(n/2) + n-1. Pokiaľ n=2k, po úprave oboch vzťahov dostaneme vzťah pre zložitosť Merge sort a to O(n) = O(n*log2n) . Spomenuté úpravy je možné nájsť v použitej literatúre[5]. |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |