 |
Algoritmy usporadúvania |
Quick sort |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |
Základné vlastnosti |
| Metóda Quick sort vynájdená pánom C.A.R. Hoare patrí medzi efektívne algoritmy usporadúvania. Už jej názov napovedá, že ide o rýchly algoritmus. Quick sort zaraďujeme medzi metódy pracujúce s operačnou zložitosťou O(n*log2n). Keďže pri tejto metóde dochádza k porovnávaniu prvkov, Quick sort patrí medzi komparačné algoritmy. Algoritmus Quick sort je univerzálny a je možné pomocou neho zoraďovať celé i reálne čísla a aj reťazce. Quick sort pracuje rekurzívne, avšak je možné tento algoritmus prepísať i do formy nerekurzívnej, ako uvidíme v nasledujúcej časti. |
Popis |
| Myšlienka metódy spočíva v postupnom rozdeľovaní poľa na dve menšie polia a v ich následnom usporiadaní. Polia sa rozdeľujú podľa náhodne zvoleného pivota. Pivot je definovaný ako prvok postupnosti, od ktorého prvky naľavo sú menšie než pivot a napravo väčšie než pivot. Je to vlastne prvok, ktorý je aj bez triedenia na svojom mieste. Matematicky: Číslo T v postupnosti x1, x2,...,xr=T,...,xn nazývame pivot, ak pre všetky i platí: pre i = 1,...,(r-1) xi < =T a pre i = (r+1), ..., n xi >= T Rekurzívne riešenie algoritmu : Vstupom pre algoritmus je neusporiadané pole a dva indexy poľa. Vstupné indexy lavy a pravy určujú, medzi ktorými indexmi sa bude postupnosť usporadúvať. V zadanej postupnosti si môžeme za pivota zvoliť ľubovolný prvok. Zvoľme prvý prvok spracúvanej časti postupnosti. Postupne prechádzame celú postupnosť a porovnávame všetky prvky s pivotom. Ak na pravej strane (presúvame sa z konca postupnosti smerom k začiatku) nájdeme prvok menší než pivot, tento prvok presunieme do ľavej (aktuálne najľavejšej) časti spracúvanej postupnosti. Postupne sa indexom približujeme k stredu postupnosti. Potom prechádzame ľavú časť (v postupnosti od začiatku smerom ku stredu). Ak v ľavej časti nájdeme prvok väčší než pivot, presunieme ho do pravej časti. Ľavým indexom sa tiež približujeme k stredu postupnosti. Za stred sa považuje miesto, kde treba zaradiť aktuálny pivot, aby sa tento nachádzal na svojom mieste. Po prejdení ľavej aj pravej časti, skontrolovaní a presunutí potrebných prvkov dáme pivot medzi tieto postupnosti, tzn., že tento prvok sa nachádza na svojom mieste (vľavo sú prvky menšie, vpravo väčšie). Rovnakým spôsobom prehľadáme a upravíme ľavú podpostupnosť a pravú podpostupnosť zvlášť, pričom pôvodný pivot si zachováva pozíciu, na ktorú bol presunutý (medzi podpostupnosti). Rekurzívnym volaním funkcie tak zabezpečíme upravenie celej postupnosti rozkladom na podpostupnosti. Môže nastať prípad, že po umiestnení pivota na jeho miesto sa tento nachádza na začiatku, resp. konci spracovávanej postupnosti, v takomto prípade je ľavá, resp. pravá podpostupnosť nulová. Vtedy je potrebné usporiadať iba druhú nenulovú podpostupnosť spracovávanej postupnosti. Rekurzívne volanie pre nulovú postupnosť sa teda nevykonáva, čo predstavuje ukončovaciu podmienku tohto algoritmu pre danú časť postupnosti. Nerekurzívne riešenie: Pred volaním funkcie usporadúvania je potrebné indexy lavy a pravy ukladať do zásobníka. Potrebu ukladania indexov do zásobníka nemožno považovať za nedostatok, pretože pri rekurzívnom volaní sú do zásobníka ukladané hodnoty všetkých lokálnych premenných, čo kladie na systém väčšie nároky. Pri nerekurzívnom riešení beží algoritmus v cykle a usporadúva čiastkové postupnosti medzi danými indexmi, pokým nie je zásobník prázdny, tzn. pokým sa v zásobníku nachádzajú hodnoty indexov lavy a pravy. |
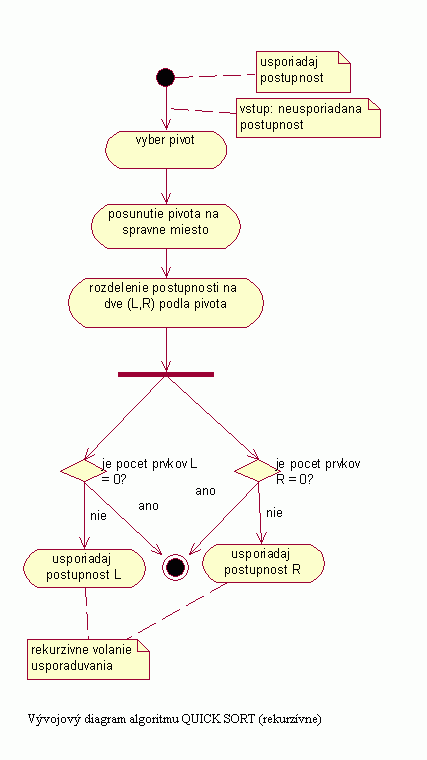
Vývojový diagram |
| Na nasledujúcom obrázku je znázornený spôsob, akým algoritmus Quick sort spracováva a usporadúva zadanú postupnosť. |
 |
Výhody a nevýhody |
| Quick sort je jednoduchý z hľadiska teoretického pochopenia, avšak problémy často nastávajú pri implementácii tohto rýchleho algoritmu. Použitím rekurzívneho riešenia Quick sort pri usporadúvaní početnej postupnosti môže v systéme dôjsť k preplneniu zásobníka, a tým k zlyhaniu usporadúvania. Quick sort je až príliš komplexný algoritmus na zoraďovanie malého počtu prvkov a pri usporadúvaní takejto postupnosti sa môže javiť ako neefektívny. |
Zložitosť |
| Tak ako pri každom algoritme, tak aj pri algoritme Quick sort, operačnú zložitosť určuje najmä počet výmen počas usporadúvania. Efektívnosť algoritmu je určená najmä výberom pivota. V najhoršom prípade dosahuje algoritmus Quick sort zložitosť O(n²), inak O(n*log2n) . Avšak i napriek najhoršiemu prípadu je Quick sort najrýchlejší algoritmus usporadúvania s pomedzi všetkých. Použitie Quick sort však nemusí byť vždy správna voľba. [2] |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |