 |
Algoritmy usporadúvania |
Quick sort |
| Porovnanie s nerekurzívnou podobou |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Štatistika algoritmu Quick sort |
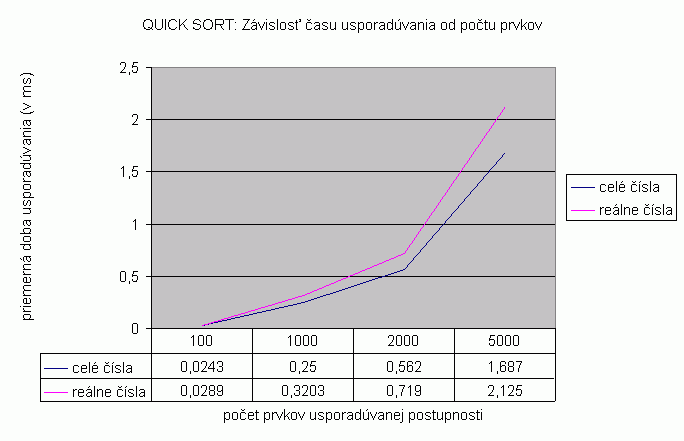
| Na nasledujúcom grafe je znázornená závislosť času usporadúvania vstupnej náhodne generovanej postupnosti od počtu a typu prvkov usporadúvanej postupnosti pre algoritmus Quick sort, rekurzívnu podobu algoritmu. Prvky sú typu celé čísla a reálne čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 100 opakovaní, pri 5 000 prvkoch 100 opakovaní. Pri usporadúvaní 10 000 prvkov systém vyhlásil chybu súvisiacu s preplnením zásobníka v dôsledku rekurzívnych volaní algoritmu Quick sort. V grafe je zreteľne vidieť rozdiel v priemernej dobe usporadúvania postupností celých a reálnych čísel už pri postupnosti s dĺžkou nad 100 prvkov. Pri postupnosti dĺžky 1 000 prvkov je rozdiel v priemernej dobe usporadúvania 0,0703 milisekúnd. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu string je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Keďže rozdiel priemerných hodnôt času usporadúvania celých či reálnych čísel a reťazcov je veľký, graf zostrojený z týchto hodnôt nebol dostatočne názorný pre porovnanie času usporadúvania celých a reálnych čísel, preto sú hodnoty času usporadúvania reťazcov zobrazené len v tabuľke. |
 |
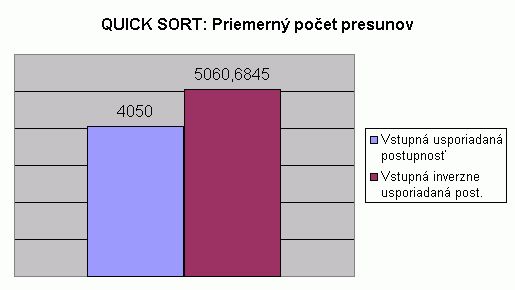
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Quick sort, rekurzívnou podobou algoritmu. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti je vyšší než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerné hodnoty počtu porovnaní pre usporadúvanie vstupnej usporiadanej aj vstupnej inverzne usporiadanej postupnosti sú neporovnateľne vyššie než hodnoty počtu porovnaní pre usporadúvanie vstupnej náhodne vygenerovanej postupnosti. Prečo je priemerný počet porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti oveľa vyšší než pri usporadúvaní vstupnej náhodne generovanej postupnosti? Algoritmus Quick sort pri hľadaní správneho miesta pre vybraný pivot prechádza aktuálnu postupnosť najskôr z "pravej", potom z "ľavej" strany a porovnáva prvky s pivotom. Pri vstupnej usporiadanej alebo inverzne usporiadanej postupnosti narastá počet porovnaní tým, že algoritmus prejde celú aktuálnu časť postupnosti z jednej zo strán, kým nájde miesto pivota. (viď príklad vizualizácie pre vstupnú usporiadanú postupnosť) |
 |
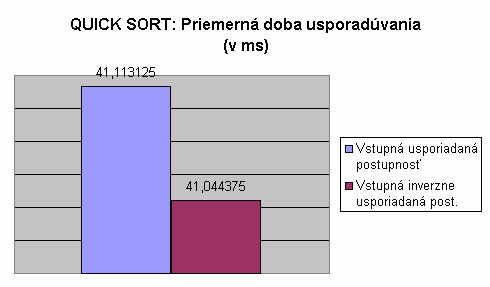
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Quick sort, rekurzívnou podobou algoritmu. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerný počet presunov pre usporiadanie vstupnej usporiadanej postupnosti nie je nulový, avšak je približne rovný počtu presunov pri usporiadaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerný počet presunov pre usporiadanie vstupnej náhodnej postupnosti je vyšší než pre usporiadanie vstupnej usporiadanej aj vstupnej inverzne usporiadanej postupnosti. Prečo je priemerný počet presunov pri usporadúvaní vstupnej usporiadanej postupnosti nenulový? Počet presunov pri usporadúvaní vstupnej usporiadanej postupnosti je rovný 2*n, čo predstavuje presun jedného prvku postupnosti vybraného za pivota do pomocnej premennej na začiatku jedného rekurzívneho volania a presun pivota na jeho miesto (pri usporiadanej postupnosti - pôvodné miesto prvku) na konci toho istého rekurzívneho volania algoritmu. (viď príklad vizualizácie pre vstupnú usporiadanú postupnosť) |
 |
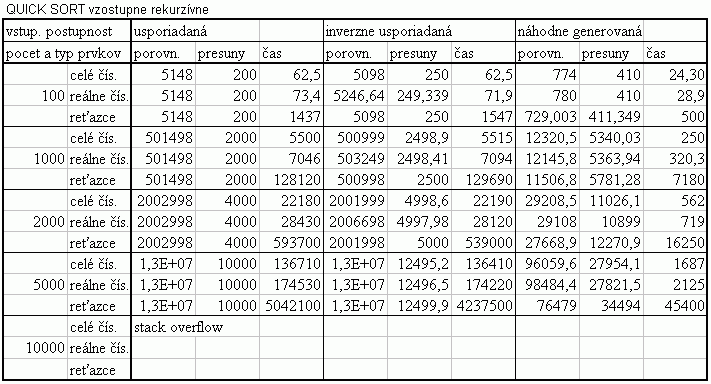
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Quick sort, rekurzívnou podobou algoritmu. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerná doba usporadúvania pre usporadúvanie vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti je približne rovnaká. V tabuľke je možné vidieť, že priemerná doba usporadúvania je pri usporadúvaní vstupnej náhodne generovanej postupnosti najnižšia, čo môže súvisieť s veľkým rozdielom v priemernom počte porovnaní, ktorý je pri vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti omnoho vyšší než pri vstupnej náhodne generovanej postupnosti. |
 |
Tabuľka štatistických hodnôt |
 |
| Porovnanie s nerekurzívnou podobou |
| Popis a zložitosť algoritmu |
| Hlavné menu |