 |
Algoritmy usporadúvania |
Quick sort |
| Späť na štatistiky |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Porovnanie rekurzvnej a nerekurzívnej podoby algoritmu Quick sort |
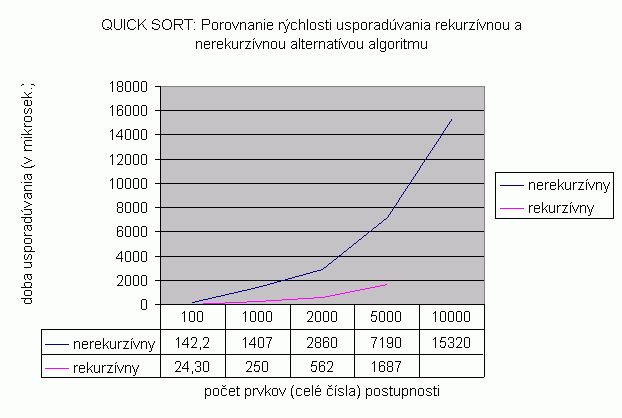
| Na tejto stránke je možné nájsť grafy porovnávajúce dve spôsoby implementácie algoritmu Quick sort. Rekurzívna a nerekurzívna podoba algoritmu sú porovnané z hľadiska rýchlosti usporadúvania, počtu porovnaní a presunov vykonaných počas usporadúvania. Na nasledujúcom grafe je znázornené porovnanie závislosti času usporadúvania vstupnej náhodne generovanej postupnosti od počtu prvkov usporadúvanej postupnosti pre rekurzívnu a nerekurzívnu podobu algoritmu Quick sort. Prvky sú typu celé čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke pre nerekurzívnu podobu algoritmu predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 100 opakovaní, pri 5 000 prvkoch 100 opakovaní a pri 10 000 prvkoch bolo spravených 10 opakovaní. Pri usporadúvaní 10 000 prvkov rekurzívnou podobou algoritmu Quick sort systém vyhlásil chybu súvisiacu s preplnením zásobníka v dôsledku rekurzívnych volaní algoritmu Quick sort. Ako môžeme vidieť v prípade nerekurzívnej alternatívy algoritmu Quick sort sme neboli obmedzení schopnosťami systému zabezpečiť rekurzívne volanie a systém bol schopný usporiadať pole aj týchto rozmerov, čo oproti rekurzívnej alternatíve predstavuje výhodu. V grafe je zreteľne vidieť rozdiel v priemernej dobe usporadúvania postupností celých čísel oboma alternatívami algoritmu Quick sort už pri postupnosti s dĺžkou 100 prvkov. Pri postupnosti dĺžky 1 000 prvkov je rozdiel v priemernej dobe usporadúvania 1157 mikrosekúnd. Vidíme teda, že usporadúvanie nerekurzívnym algoritmom Quick sort je pomalšie než rekurzívnym, avšak výhodou nerekurzívnej podoby stále zostáva schopnosť usporiadať pole s počtom prvkov nad 5 000. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu reálne čísla a reťazec je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Pri zobrazení týchto hodnôt v grafe spolu s hodnotami získanými meraniami rekurzívneho algoritmu Quick sort by sme získali podobný výsledok ako v grafe zobrazujúcom rýchlosť usporadúvania celých čísel. |
 |
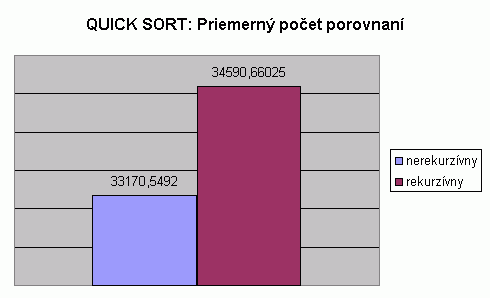
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej náhodne generovanej postupnosti celých čísel rekurzívnou a nerekurzívnou podobou algoritmu Quick sort. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti pre nerekurzívnu podobu algoritmu Quick sort. V nasledujúcom grafe vidíme, že priemerný počet porovnaní pri použití rekurzívnej alternatívy je vyšší než pri použití nerekurzívnej alternatívy algoritmu Quick sort. Tento rozdiel však predstavuje iba približne 1420 porovnaní, čo je spôsobené náhodnosťou generovania vstupnej postupnosti. Keďže obe alternatívy majú jadro implementácie totožné, nemožno ich na základe počtu porovnaní rozlišovať, prípadne určovať ktorých z nich je z tohto hľadiska lepší. |
 |
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej náhodne generovanej postupnosti celých čísel rekurzívnou a nerekurzívnou podobou algoritmu Quick sort. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti pre nerekurzívnu podobu algoritmu Quick sort. V grafe vidíme, že priemerný počet presunov pri použití nerekurzívnej alternatívy je vyšší než pri použití rekurzívnej alternatívy algoritmu Quick sort, avšak rozdiel je len 5 presunov. Tak ako bolo spomínané pri predchádzajúcom grafe je tento rozdiel spôsobený náhodnosťou generovania vstupnej postupnosti. Keďže obe alternatívy majú jadro implementácie totožné, nemožno ich na základe počtu presunov rozlišovať, prípadne určovať ktorých z nich je z tohto hľadiska lepší, čo nám vlastne dokazuje aj zanedbateľný rozdiel v počte presunov pri použití dvoch alternatív algoritmu Quick sort. |
 |
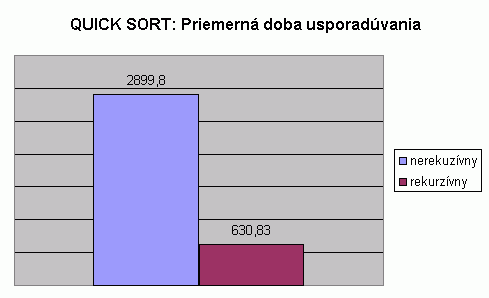
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej náhodne generovanej postupnosti celých čísel rekurzívnou a nerekurzívnou podobou algoritmu Quick sort. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti pre nerekurzívnu podobu algoritmu Quick sort. V grafe vidíme, že priemerná doba usporadúvania pri použití nerekurzívnej podoby algoritmu je oveľa vyššia než pri použití rekurzívnej podoby, čo už bolo popísané pri prvom grafe na tejto stránke. Tento rozdiel pri priemere z času usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 prvkami dvoma alternatívami algoritmu Quick sort je 2268,97 mikrosekúnd. |
 |
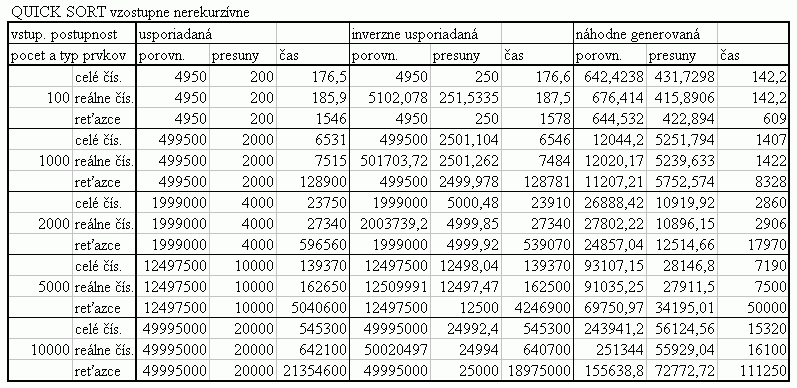
Tabuľka štatistických hodnôt |
 |
| Späť na štatistiky |
| Popis a zložitosť algoritmu |
| Hlavné menu |