 |
Algoritmy usporadúvania |
Shell sort |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |
Základné vlastnosti |
| Shell sort je algoritmus určený na usporadúvanie postupnosti prvkov, pomenovaný podľa svojho autora Donalda Shella. Zaraďujeme ho do skupiny algoritmov pracujúcich s operačnou zložitosťou O(n²). Shell sort je najefektívnejší avšak i najzložitejší algoritmus z tejto skupiny. [2] Pri tejto metóde dochádza k porovnávaniu prvkov, preto Shell sort zaraďujeme medzi komparačné algoritmy. Algoritmus je univerzálny a je možné pomocou neho zoraďovať celé i reálne čísla a aj reťazce. |
Popis |
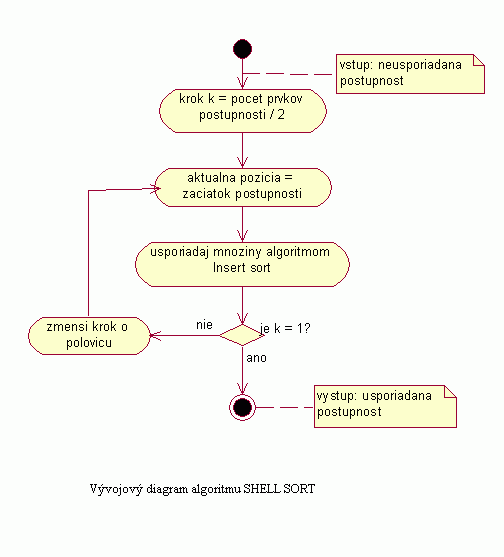
| Pri usporadúvaní algoritmom Shell sort si na začiatku určíme nejaký krok. Spravidla sa počiatočný krok určí ako polovica počtu prvkov usporadúvanej postupnosti, teda krok k=n/2. Podľa hodnoty k algoritmus Shell sort vytvorí množiny. Počet množín sa rovná hodnote k. Do množiny zaraďujeme tie prvky usporadúvanej postupnosti, ktoré sú na každej k-tej pozícii. Napríklad do prvej množiny pri hodnote kroku k=3 zaradíme prvky na pozíciách 1, 4, 7... , do druhej množiny by patrili prvky na pozíciách 2, 5, 8... a posledná tretia množina by obsahovala prvky na pozíciách 3, 6, 9... Takto rozdelíme prvky usporadúvanej postupnosti do k množín až po posledný prvok. Jednotlivé množiny sú spravidla usporadúvané algoritmom Insert sort. Po usporiadaní jednotlivých množín sú prvky v celkovej postupnosti usporiadané vzhľadom na pozície, z ktorých boli prvky do danej množiny zaradené. Celková postupnosť však nemusí byť usporiadaná. S krokom k zmenšeným o polovicu pôvodnej hodnoty kroku Shell sort opäť vytvorí množiny a pokračuje ďalej v usporadúvaní už spomenutým spôsobom. Algoritmus Shell sort končí po prejdení postupnosti s krokom k=1. Výstupné usporiadanie je závislé od spôsobu usporiadania jednotlivých skupín algoritmom Insert Sort, ak použijeme vzostupné (zostupné) usporiadanie v rámci skupín, bude i výsledné usporiadanie vzostupné (zostupné). |
Vývojový diagram |
| Na nasledujúcom obrázku je znázornený vývojový diagram pre algoritmus Shell sort, ktorý názorne popisuje spracovanie a usporadúvanie postupnosti týmto algoritmom. Uvedený diagram je možné aplikovať pri implementovaní vzostupného i zostupného usporadúvania postupnosti. Rozlíšenie týchto dvoch usporadúvaní sa deje pri porovnaní dvoch prvkov postupnosti. Kritérium porovnania si môžeme ľubovolne určiť podľa želaného výstupného usporiadania. |
 |
Výhody a nevýhody |
| Shell sort je najrýchlejší algoritmus zo všetkých spomínaných algoritmov patriacich do skupiny zložitosti O(n²). Pokiaľ porovnávame Shell sort s jeho konkurentmi v tejto skupine, je viac ako päťkrát rýchlejší než Bubble sort a dvakrát rýchlejší než Insert sort. Spomalenie metódy sa prejavuje až pri usporadúvaní postupnosti s viac ako 5000 prvkami. [2] |
Zložitosť |
| Keďže algoritmus Shell sort pri usporadúvaní prvkov v skupine využíva algoritmus Insert sort, je jeho zložitosť od tohto algoritmu závislá. Ako už bolo spomínané a dokazované Insert sort pracuje so zložitosťou O(n²). Mohlo by sa zdať, že určiť zložitosť algoritmu Shell sort je jednoduché pri vychádzaní z týchto skutočností. Opak je však pravdou. Na štúdium tohto algoritmu bolo počas posledných niekoľko desiatok rokov vynaložené značné úsilie, dodnes nikto nevie, aký najlepší možný krok použiť v jednotlivých prechodoch postupnosťou pre veľký počet usporadúvaných prvkov. [10] Keďže viaceré zdroje a výskumy sa líšia v posúdení zložitosti algoritmu Shell sort, je táto častokrát uvádzaná ako O(n²). Časová náročnosť Shell sort závisí od voľby začiatočného kroku. [7] |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |