 |
Algoritmy usporadúvania |
Bubble sort |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |
Základné vlastnosti |
| Bubble sort je algoritmus určený na usporadúvanie postupnosti prvkov.
Operačná zložitosť algoritmu je O(n²). Je to najstarší, najjednoduchší, avšak i najpomalší algoritmus zo skupiny algoritmov s operačnou zložitosťou O(n²). Bubble sort je dnes prakticky nepoužívaný, avšak vďaka svojej jednoduchosti prežíva ako príklad jednoduchého usporadúvania vo výučbových procesoch. Pri tejto metóde dochádza k porovnávaniu prvkov, čiže i Bubble sort patrí medzi komparačné algoritmy. Algoritmus Bubble sort je univerzálny a je možné pomocou neho zoraďovať celé i reálne čísla a aj reťazce. |
Popis |
| Vstupom pre algoritmus Bubble sort je neusporiadaná postupnosť. Algoritmus postupne prechádza celú postupnosť a porovnáva dva susedné prvky, v prípade potreby ich vymení. Pokiaľ v postupnosti dochádza k výmene prvkov, Bubble sort opätovne prechádza celú postupnosť a porovnáva všetky prvky usporadúvanej postupnosti. Ak pri prejdení celej postupnosti nenastane žiadna výmena, postupnosť je usporiadaná. Bubble sort je možné použiť pre usporadúvania vzostupne i zostupne. Rozlíšenie týchto dvoch usporadúvaní sa deje pri porovnaní dvoch prvkov postupnosti. Kritérium porovnania si môžeme ľubovolne určiť podľa želaného výstupného usporiadania. |
Vývojový diagram |
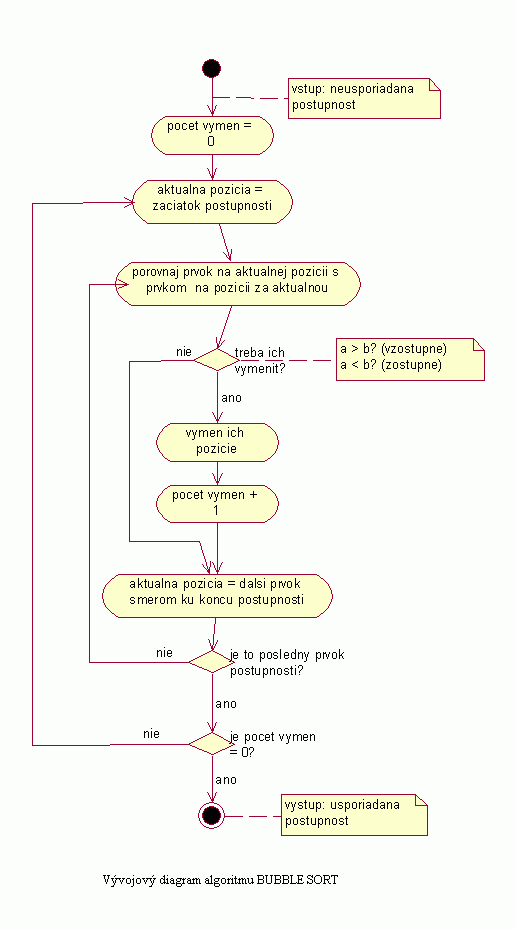
| Na nasledujúcom obrázku je znázornený vývojový diagram pre algoritmus Bubble sort, ktorý názorne popisuje spracovanie a usporadúvanie postupnosti týmto algoritmom. Uvedený diagram je možné aplikovať pri usporadúvaní postupnosti vzostupne i zostupne. |
 |
Výhody a nevýhody |
| Výhodou algoritmu Bubble sort je jeho jednoduchosť. Zo skupiny algoritmov so zložitosťou O(n²) je Bubble sort najmenej efektívny. Pomalosť algoritmu sa prejavuje už pri usporadúvaní viac ako sto prvkov. [2] Jednoduchosť a vysoká neefektívnosť robia z algoritmu Bubble sort prakticky nepoužívaný algoritmus. Avšak vďaka svojej jednoduchosti, názornosti a histórii Bubble sort prežíva ako učebnicový príklad. |
Zložitosť |
| Počet operácii porovnania je pri každom prechode cez usporadúvanú postupnosť (n-1) . Počet celkových prechodov cez postupnosť je závislý na hodnotách usporadúvaných prvkov. Pokiaľ pri prechode postupnosťou nedôjde k výmene prvkov, je postupnosť zoradená. Minimálny počet prechodov cez postupnosť je 1 pre usporiadanú vstupnú postupnosť a maximálny počet prechodov je n-1 pre inverzne usporiadanú vstupnú postupnosť. Odtiaľ priemerný počet prechodov cez postupnosť je ( 1+(n-1) )/2 = n/2. Po usporiadaní postupnosti je teda celkový počet porovnaní v priemere rovný: n/2*(n-1) = 1/2*(n² - n) . Počet presunov prvkov pri usporiadanej vstupnej postupnosti je samozrejme 0. Maximálny počet presunov môžeme dostať, ak pri každom porovnaní dôjde k výmene. Keďže priemerný počet porovnaní po usporiadaní celej postupnosti je 1/2*(n² - n) , maximálny počet výmen je: 3*1/2*(n² - n) , kde násobenie tromi znamená presun jedného prvku do pomocnej premennej (1*), presun prvého prvku na miesto druhého (2*), presun prvku z pomocnej premennej na pôvodné miesto prvého prvku (3*). [1] Z počtu porovnaní a maximálneho počtu výmen prvkov vidíme, že operačná zložitosť algoritmu Bubble sort je O(n²). |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |