 |
Algoritmy usporadúvania |
Bubble sort |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Štatistika algoritmu Bubble sort |
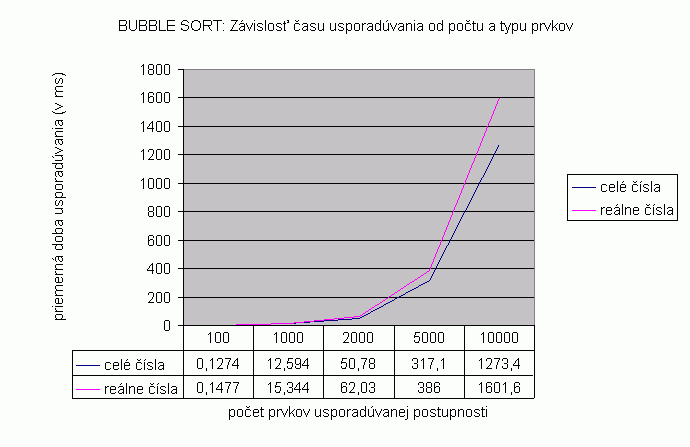
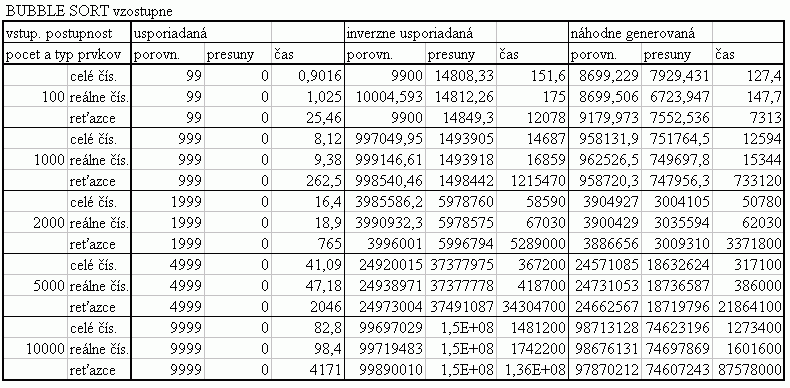
| Na nasledujúcom grafe je znázornená závislosť času usporadúvania vstupnej náhodne generovanej postupnosti od počtu a typu prvkov usporadúvanej postupnosti pre algoritmus Bubble sort. Prvky sú typu celé čísla a reálne čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 100 opakovaní, pri 5 000 prvkoch 100 opakovaní a pri 10 000 prvkoch bolo spravených 10 opakovaní. Pri usporadúvaní vstupnej usporiadanej postupnosti bol algoritmus Bubble sort príliš rýchly a vyššie uvedené počty opakovaní neboli dostačujúce na zachytenie štatistík, preto pri usporadúvaní vstupnej usporiadanej postupnosti pri všetkých dĺžkach vstupných postupností bol počet opakovaní zvýšený aj o 3 rády pre usporadúvanie čísel a o jeden rád pre usporadúvanie reťazcov. Pri usporadúvaní postupnosti dĺžky 5 000 prvkov bolo naopak potrebné znížiť počet opakovaní o 1 rád pri usporadúvaní vstupnej inverzne usporiadanej a náhodne vygenerovanej postupnosti. Pri usporadúvaní postupnosti s 10 000 reťazcami bolo možné vykonať len jedno opakovanie z dôvodu príliš dlhého trvania vykonávania algoritmu pri viacerých opakovaniach. Podľa hodnôt je vidieť, že usporadúvanie reálnych čísel trvá dlhšie než usporadúvanie celých čísel. V grafe je rozdiel v priemernom čase usporadúvania zreteľne rozoznateľný až pri postupnosti s viac ako 2 000 prvkami, pričom pri usporadúvaní postupnosti s 5 000 prvkami je rozdiel priemerných hodnôt času usporadúvania postupnosti celých a reálnych čísel rovný 68,9 milisekúnd. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu string je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Keďže rozdiel priemerných hodnôt času usporadúvania celých či reálnych čísel a reťazcov je veľký, graf zostrojený z týchto hodnôt nebol dostatočne názorný pre porovnanie času usporadúvania celých a reálnych čísel, preto sú hodnoty času usporadúvania reťazcov zobrazené len v tabuľke. |
 |
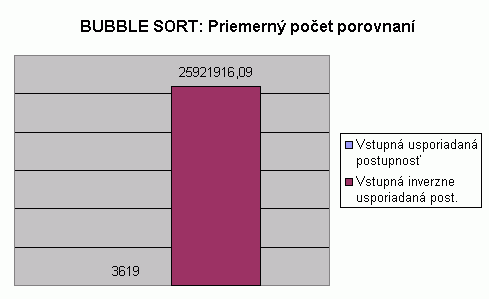
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Bubble sort. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti je neporovnateľne nižší než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerné hodnoty počtu porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti sú takisto neporovnateľne nižšie než hodnoty pre usporadúvanie vstupnej náhodne vygenerovanej postupnosti. Keďže pri usporadúvaní vstupnej usporiadanej postupnosti algoritmus prejde usporadúvanú postupnosť len jeden krát, a pritom porovná susedné prvky je priemerný počet porovnaní rovný (n-1). Vstupná inverzne usporiadaná postupnosť je pre algoritmus Bubble sort najhorším prípadom, čo vysvetluje aj veľký rozdiel v priemernom počte porovnanív nasledujúcom grafe. |
 |
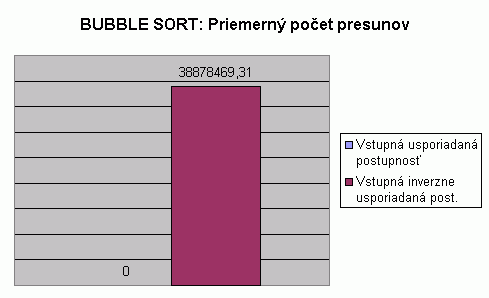
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Bubble sort. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerný počet presunov pre usporiadanie vstupnej usporiadanej postupnosti je nulový, zatiaľ čo priemerný počet presunov pri usporiadaní vstupnej inverzne usporiadanej postupnosti je omnoho vyšší. Pri pohľade do tabuľky zistíme, že priemerný počet presunov pre usporiadanie vstupnej náhodnej postupnosti je približne o polovicu menší než pre usporiadanie vstupnej inverzne usporiadanej postupnosti. Z toho nám vyplýva, že usporiadaná postupnosť je pre algoritmus Bubble sort najlepším vstupom a inverzne usporiadaná postupnosť naopak najhorším vstupom. |
 |
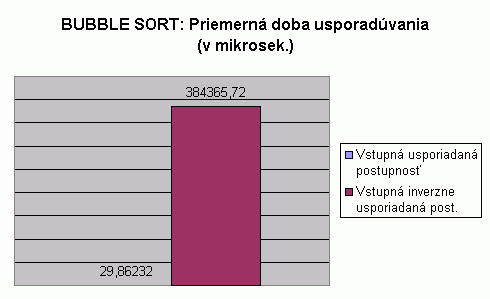
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Bubble sort. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerná doba usporadúvania pre usporadúvanie vstupnej usporiadanej postupnosti je neporovnateľne nižšia než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti, čo má jednoznačnú súvislosť s rozdielnym priemerným počtom porovnaní a presunov. Túto súvislosť je možno dobre vidieť v nižšie uvedenej tabuľke. V tabuľke je takisto vidieť, že priemerná doba usporadúvania vstupnej náhodne vygenerovanej postupnosti je nižšia než priemerná doba usporadúvania vstupnej inverzne usporiadanej postupnosti, čo nám opäť potvrdzuje fakt, že inverzne usporiadaná postupnosť je pre algoritmus Bubble sort najhorším vstupom. |
 |
Tabuľka štatistických hodnôt |
 |
| Popis a zložitosť algoritmu |
| Hlavné menu |