 |
Algoritmy usporadúvania |
Insert sort |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-inverzne usporiadaný vstup | ||||
| Štatistika algoritmu |
Základné vlastnosti |
| Metóda Insert sort, určená na usporadúvanie postupnosti prvkov vkladaním, patrí medzi jednoduché algoritmy usporadúvania. Algoritmus Insert sort pracuje s operačnou zložitosťou O(n²). Pri tejto metóde dochádza k porovnávaniu prvkov, preto patrí medzi komparačné algoritmy. Algoritmus Insert sort je univerzálny a je možné pomocou neho zoraďovať celé i reálne čísla a aj reťazce. |
Popis |
| Pri zoraďovaní postupnosti o n prvkoch metóda zaručuje a zároveň využíva, že prvky 1 až i (na začiatku i = 2) sú už zoradené. Postupne prejdeme celú postupnosť od i = 2 až po i < n, každý prvok na pozícii i ukladáme do dočasnej premennej. Porovnávaním zistíme, na ktoré miesto v postupnosti s indexmi 1 až i-1 daný prvok patrí a vložíme ho tam. Takto je zaručené, že i po vložení prvku do postupnosti s indexmi 1 až i-1 zostáva táto postupnosť zoradená. Usporiadanie je ukončené po zaradení posledného prvku. Uvedený spôsob usporadúvania je možné realizovať pre vzostupné i zostupné usporiadanie. Konkrétne usporiadanie môžeme docieliť zmenou podmienok pri porovnávaní prvkov. |
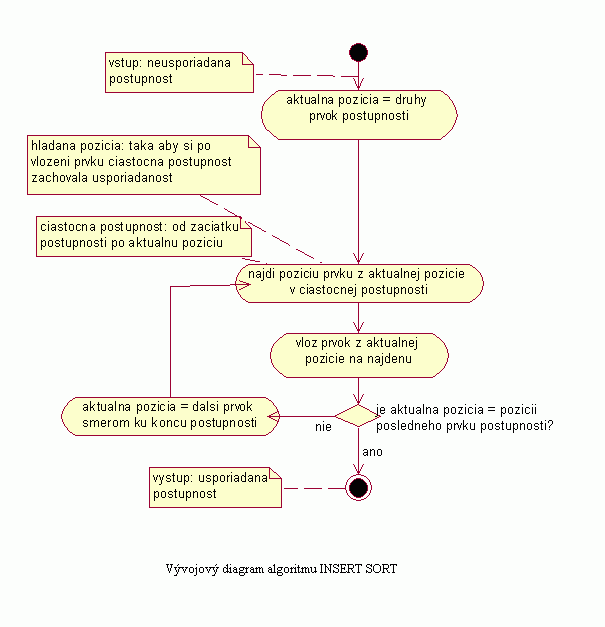
Vývojový diagram |
| Na nasledujúcom obrázku je znázornený vývojový diagram pre algoritmus Insert sort, ktorý názorne popisuje spracovanie a usporadúvanie postupnosti týmto algoritmom. Uvedený diagram je možné aplikovať pri usporadúvaní postupnosti vzostupne i zostupne. Rozlíšenie týchto dvoch usporadúvaní sa deje pri hľadaní pozície v čiastočnej už usporiadanej postupnosti, ktoré nie je v diagrame podrobnejšie popísané. Kritérium pre hľadanú pozíciu môžeme určiť podľa želaného výstupného usporiadania. |
 |
Výhody a nevýhody |
| Veľkými výhodami algoritmu Insert sort sú jeho jednoduchosť a efektívnosť. Pri porovnaní s inými algoritmami je Insert sort približne dvakrát rýchlejší než Bubble sort a približne o 40% rýchlejší než Select sort. Avšak pri usporadúvaní postupností s veľkým počtom prvkov je i Insert sort neefektívny. [2] |
Zložitosť |
| Keďže pri Insert sort dochádza k ukladaniu vkladaného prvku do dočasnej premennej, náročnosť tejto operácie zvyšuje (pamäťovú) náročnosť usporadúvania. Na náročnosť algoritmu má taktiež vplyv presúvanie prvkov v rámci usporadúvanej postupnosti. Počet operácii porovnania v i-tom kroku je najmenej 1 a najviac i, priemerne (i+1)/2. Po usporiadaní celej postupnosti, po n-1 krokoch, je počet porovnaní : minimálne : (n-1)*1 = (n-1) maximálne : |
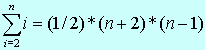 |
|
Počet operácii presunu prvkov je v i-tom kroku o 2 väčší než počet porovnaní : minimálne : 3*(n-1) maximálne : |
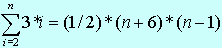 |
|
Podľa vzťahov pre najhoršie prípady vidíme, že operačná zložitosť algoritmu Insert sort je O(n²). [1] I keď zložitosť Insert sort je rovnaká ako zložitosť Bubble sort, Insert sort je dvakrát efektívnejší (rýchlejší) než Bubble sort a približne o 40% rýchlejší než Select sort. Spomalenie metódy je pozorovateľné pri usporadúvaní postupnosti s viac ako 2000 prvkami. [2] |
| Hlavné menu | Predchádzajúci | Nasledujúci | ||
| Implementácia | ||||
| Vizualizácia-náhodný vstup | ||||
| Vizualizácia-usporiadaný vstup | ||||
| Štatistika algoritmu |