 |
Algoritmy usporadúvania |
Select sort |
| Hlavné menu | Nasledujúci | |
| Implementácia | ||
| Vizualizácia-náhodný vstup | ||
| Vizualizácia-usporiadaný vstup | ||
| Štatistika algoritmu |
Základné vlastnosti |
| Metóda Select sort je algoritmus určený na usporadúvanie postupnosti. Je veľmi jednoduchý na implementáciu. Select sort patrí medzi pomalšie algoritmy pracujúce s operačnou zložitosťou O(n²). Pri tejto metóde dochádza k porovnávaniu prvkov, preto Select sort patrí medzi komparačné algoritmy. Algoritmus Select sort je univerzálny a je možné pomocou neho zoraďovať celé i reálne čísla a aj reťazce. |
Popis |
| Select sort je algoritmus usporadúvania výberom maximálneho alebo minimálneho prvku z neusporiadanej časti postupnosti. Pri prvom hľadaní algoritmus prejde celú zadanú postupnosť a nájde minimálny prvok. Nájdený prvok vymení s prvým prvkom postupnosti. Usporadúvané pole skráti o jeden práve usporiadaný prvok. Algoritmus v ďalšom kroku hľadá minimálny prvok v skrátenej ešte neusporiadanej postupnosti a po zaradení ďalšieho prvku na správne miesto je postupnosť opäť skrátená. Takto pokračuje až po posledný prvok. Uvedený spôsob usporiada postupnosť vzostupne. Pri vykonávaní algoritmu môžeme vyberať maximálny alebo minimálny prvok ešte neusporiadanej postupnosti a zoraďovať prvky na začiatku alebo na konci postupnosti, tým máme možnosť zoradiť postupnosť vzostupne alebo zostupne rôznymi spôsobmi. |
Vývojový diagram |
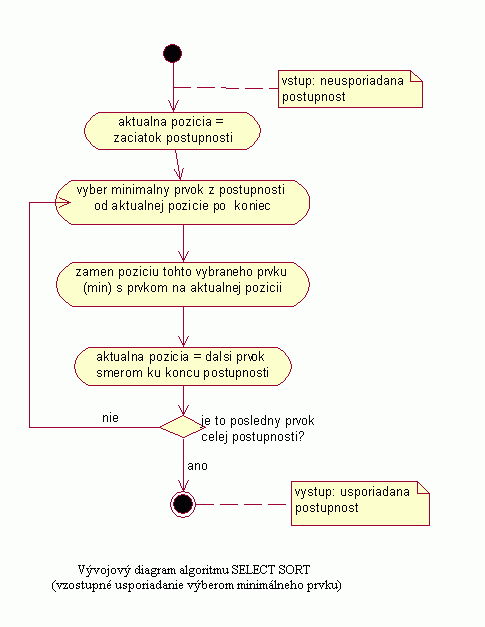
| Na nasledujúcom obrázku je znázornený vývojový diagram pre algoritmus Select sort, ktorý názorne popisuje spracovanie a usporadúvanie postupnosti týmto algoritmom. Uvedený diagram znázorňuje usporiadanie vstupnej postupnosti vzostupne výberom minimálneho prvku. |
 |
Výhody a nevýhody |
| Najväčšia výhoda Select sort spočíva v jeho jednoduchosti, avšak je veľmi neefektívny, preto je výhodné ho nahradiť takisto jednoduchým avšak efektívnejším algoritmom Insert sort. Keďže pri usporadúvaní algoritmom Select sort vyberáme maximálny alebo minimálny prvok, môže pri usporadúvaní nenumerických prvkov nastať problém ako určiť maximum, resp. minimum. V prípade použitia jazyka C/C++ však takýto problém nastať nemôže, pretože vieme určiť veľkosť celých i reálnych čísel a dokonca aj reťazcov. |
Zložitosť |
| Operačnú zložitosť pri algoritme Select sort určuje najmä počet porovnaní a výmen počas usporadúvania. Algoritmus Select sort sa postupne aplikuje na postupnosti dĺžky n, n-1, n-2 až 2, kde n je dĺžka vstupnej neusporiadanej postupnosti. V každej z postupností hľadáme minimálny (príp. maximálny) prvok danej postupnosti, pričom počet porovnaní v postupnosti dĺžky n je n-1, v n-1 dlhej postupnosti je to n-2 porovnaní atď. Takže po usporiadaní celej postupnosti bude celkový počet porovnaní rovný (n² - n)/2. Tu vidíme, že zložitosť algoritmu je skutočne O(n²). [1] Keďže celkovo vzájomne vymeníme n-1 prvkov, počet výmen je celkovo rovný (n-1) + (n-1) + (n-1) = 3*(n-1), kde prvé (n-1) predstavuje presun prvku A do pomocnej premennej, druhé (n-1) je presun druhého z vymieňaných prvkov B do postupnosti na pôvodnú pozíciu A, posledné (n-1) predstavuje finálny presun A na pôvodné miesto B, a tým sú prvky zamenené. [1] |
| Hlavné menu | Nasledujúci | |
| Implementácia | ||
| Vizualizácia-náhodný vstup | ||
| Vizualizácia-usporiadaný vstup | ||
| Štatistika algoritmu |