 |
Algoritmy usporadúvania |
Select sort |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Štatistika algoritmu Select sort |
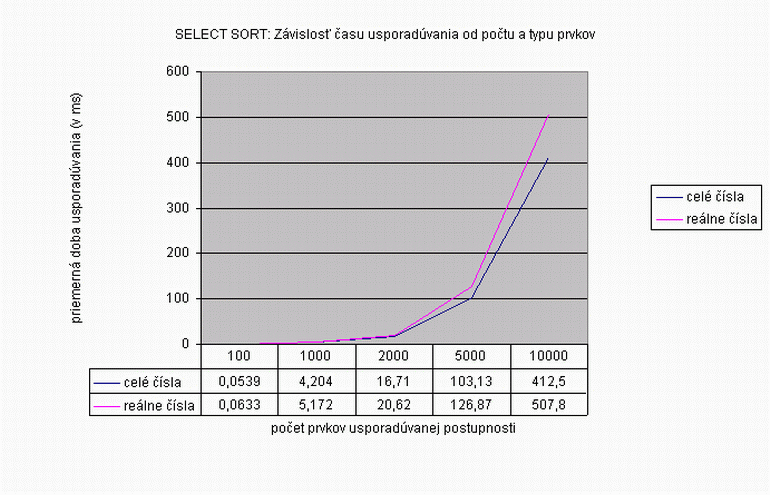
| Na nasledujúcom grafe je znázornená závislosť času usporadúvania vstupnej náhodne generovanej postupnosti od počtu a typu prvkov usporadúvanej postupnosti pre algoritmus Select sort. Prvky sú typu celé čísla a reálne čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 100 opakovaní, pri 5 000 prvkoch 100 opakovaní a pri 10 000 prvkoch bolo spravených 10 opakovaní. Podľa hodnôt je vidieť, že usporadúvanie reálnych čísel trvá dlhšie než usporadúvanie celých čísel. V grafe môžeme zreteľne vidieť rozdiel v priemernom čase usporadúvania až pri postupnosti s viac ako 2 000 prvkami, pričom pri usporadúvaní postupnosti s 5 000 prvkami je rozdiel priemerných hodnôt času usporadúvania postupnosti celých a reálnych čísel rovný 23,74 milisekúnd. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu string je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Usporadúvanie reťazcov je náročnejšie na operácie porovnania a na pamäť, preto počet opakovaní pri usporadúvaní reťazcov musel byť pre všetky dĺžky usporadúvanej postupnosti až o rád nižší než pri usporadúvaní čísel z dôvodu príliš dlhého času usporadúvania pri zachovaní pôvodných počtov opakovaní. Keďže rozdiel priemerných hodnôt času usporadúvania celých či reálnych čísel a reťazcov je veľký, graf zostrojený z týchto hodnôt nebol dostatočne názorný pre porovnanie času usporadúvania celých a reálnych čísel, preto sú hodnoty času usporadúvania reťazcov zobrazené len v tabuľke. |
 |
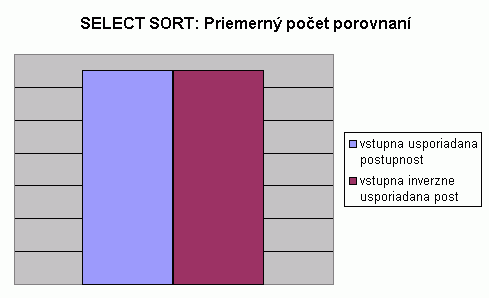
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Select sort. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet porovnaní je pre usporadúvanie vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti rovnaký. Pri pohľade do tabuľky zistíme, že priemerné hodnoty počtu porovnaní sú rovnaké pre usporadúvanie lubovoľnej vstupnej postupnosti rovnakej dĺžky. Prečo je tento priemerný počet porovnaní pri usporadúvaní postupnosti algoritmom Select sort rovnaký? Algoritmus hľadá minimá (resp. maximá) v ešte neusporiadanej časti postupnosti. Postupne porovnáva prvky tejto časti postupnosti s aktuálnym minimom, keďže dĺžka vstupnej postupnosti je nemenná, je priemerný počet porovnaní takisto nemenný. |
 |
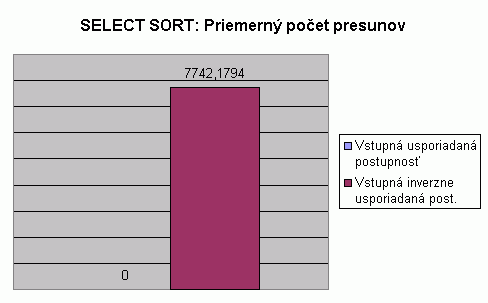
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Select sort. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet presunov pre usporadúvanie vstupnej usporiadanej postupnosti je nulový a vstupnej inverzne usporiadanej postupnosti je rovný približne 7742. Nulová hodnota pri usporadúvaní vstupnej usporiadanej postupnosti a nenulová hodnota pri usporadúvaní vstupnej inverzne usporadúvanej postupnosti sú očakávané. Avšak pri pohľade do tabuľky zistíme, že priemerný počet presunov pre usporiadanie vstupnej inverzne usporiadanej postupnosti je menší než pre usporiadanie vstupnej náhodnej vygenerovanej postupnosti, hoci by sa mohlo zdať, že vstupná inverzne usporiadaná postupnosť je horší prípad vstupu než náhodne vygenerovaná postupnosť. Prečo je počet presunov algoritmu Select sort pri usporadúvaní vstupnej postupnosti inverzne usporiadanej v priemere menší než pri náhodne generovanej vstupnej postupnosti? Po usporiadaní prvej polovice vstupnej postupnosti nastane situácia, že všetky prvky druhej polovice postupnosti sú už na svojom mieste, tzn. už nedochádza k ďalším presunom. Inkrementuje sa len počet porovnaní pri hľadaní minima (resp. maxima) v ostávajúcej časti postupnosti. (viď príklad vizualizácie pre vstupnú inverzne usporiadanú postupnosť) |
 |
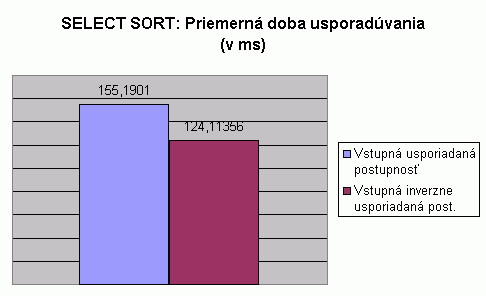
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Select sort. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerná doba usporadúvania pre usporadúvanie vstupnej usporiadanej postupnosti je vyššia než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. |
 |
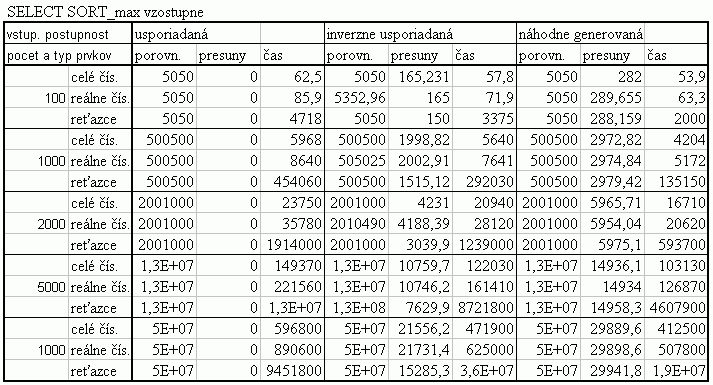
Tabuľka štatistických hodnôt |
 |
| Popis a zložitosť algoritmu |
| Hlavné menu |