 |
Algoritmy usporadúvania |
Insert sort |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Štatistika algoritmu Insert sort |
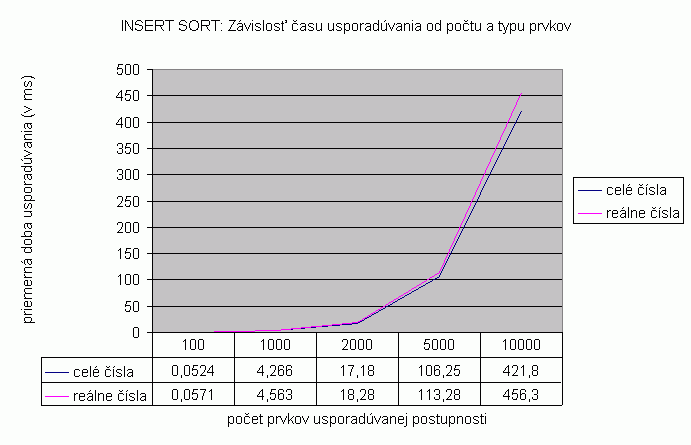
| Na nasledujúcom grafe je znázornená závislosť času usporadúvania vstupnej náhodne generovanej postupnosti od počtu a typu prvkov usporadúvanej postupnosti pre algoritmus Insert sort. Prvky sú typu celé čísla a reálne čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 100 opakovaní, pri 5 000 prvkoch 100 opakovaní a pri 10 000 prvkoch bolo spravených 10 opakovaní. Podľa hodnôt je vidieť, že usporadúvanie reálnych čísel trvá dlhšie než usporadúvanie celých čísel. V grafe je rozdiel v priemernom čase usporadúvania rozoznateľný až pri postupnosti s viac ako 2 000 prvkami, pričom pri usporadúvaní postupnosti s 5 000 prvkami je rozdiel priemerných hodnôt času usporadúvania postupnosti celých a reálnych čísel rovný 7,03 milisekúnd a pri postupnosti s 10 000 prvkami je tento rozdiel iba 34,5 milisekúnd. Môžeme teda povedať, že usporadúvanie celých a reálnych čísel algoritmom Insert sort je z pohľadu priemernej doby usporadúvania porovnateľné. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu string je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Usporadúvanie reťazcov je náročnejšie na operácie porovnania a na pamäť, preto počet opakovaní pri usporadúvaní reťazcov musel byť pre všetky dĺžky usporadúvanej postupnosti až o rád nižší než pri usporadúvaní čísel z dôvodu príliš dlhého času usporadúvania pri zachovaní pôvodných počtov opakovaní. Keďže rozdiel priemerných hodnôt času usporadúvania celých či reálnych čísel a reťazcov je veľký, graf zostrojený z týchto hodnôt nebol dostatočne názorný pre porovnanie času usporadúvania celých a reálnych čísel, preto sú hodnoty času usporadúvania reťazcov zobrazené len v tabuľke. |
 |
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Insert sort. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti je neporovnateľne vyšší než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerné hodnoty počtu porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti sú takisto neporovnateľne vyššie než hodnoty pre usporadúvanie vstupnej náhodne vygenerovanej postupnosti. Prečo je priemerný počet porovnaní pri usporadúvaní vstupnej usporiadanej postupnosti taký vysoký? Pre vkladaný prvok sa snažíme v už usporiadanej časti postupnosti nájsť jeho miesto. Vkladaný prvok porovnávame s prvkami v tejto časti postupnosti. Keďže prvok je pri vstupnej usporiadanej postupnosti na svojom mieste, porovnávame ho so všetkými prvkami v už usporiadanej časti postupnosti, čím nám vzniká vysoký počet porovnaní. Z hľadiska počtu porovnaní je vstupná usporiadaná postupnosť pre Insert sort najhorším prípadom. (zelené zvýraznenie) Prečo je priemerný počet porovnaní usporadúvania vstupnej inverzne usporiadanej postupnosti oveľa nižší než pri usporadúvaní náhodne generovanej postupnosti (resp. vstupnej usporiadanej postupnosti)? Pri vstupnej inverzne usporiadanej postupnosti je každý vkladaný prvok menší než prvok na začiatku už usporiadanej časti postupnosti, tým dochádza len k jednému porovnaniu a následnému vloženiu prvku na začiatok tejto časti postupnosti. S tým súvisí i vyšší priemerný počet presunov pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. Keďže vkladaný prvok zaraďujeme na začiatok už usporiadanej časti postupnosti, všetky prvky v tejto časti musíme presúvať o jedno miesto ďalej, tým nám narastá počet presunov. (viď príklad vizualizácie pre vstupnú inverzne usporiadanú postupnosť) |
 |
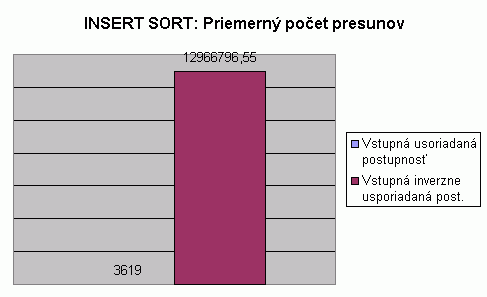
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Insert sort. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerný počet presunov pre usporiadanie vstupnej usporiadanej postupnosti nie je nulový, avšak je neporovnateľne nižší než pri usporiadaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerný počet presunov pre usporiadanie vstupnej náhodnej postupnosti je menší než pre usporiadanie vstupnej inverzne usporiadanej postupnosti. Prečo pri usporadúvaní vstupnej usporiadanej postupnosti nie je počet presunov nulový? Pri algoritme Insert sort si práve vkladaný prvok ukladáme do pomocnej premennej, inkrementujeme počet presunov, aj keď sa nejedná o presun v rámci postupnosti. Po porovnaní s prvkami v už usporiadanej časti postupnosti zisťujeme, že tento prvok je na správnom mieste, nie sú potrebné ďalšie presuny. Počet presunov pre usporiadanie vstupnej usporiadanej postupnosti je rovný n-1. |
 |
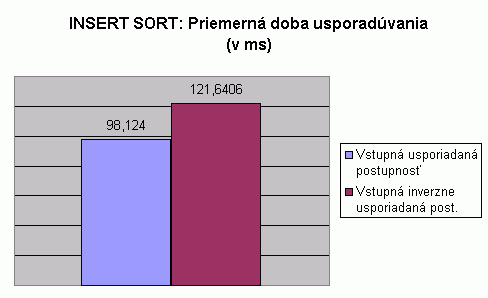
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Insert sort. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerná doba usporadúvania pre usporadúvanie vstupnej usporiadanej postupnosti je nižšia než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. V tabuľke je možné vidieť, že pri usporadúvaní vstupnej usporiadanej postupnosti je vyšší počet porovnaní a pri usporadúvaní vstupnej inverzne usporiadanej postupnosti je vyšší počet presunov. Keďže priemerná doba usporadúvania je vyššia pri usporadúvaní vstupnej inverzne usporiadanej postupnosti, môžeme usudzovať, že operácia presunu celých čísel je časovo náročnejšia než operácia porovnania dvoch celých čísel. |
 |
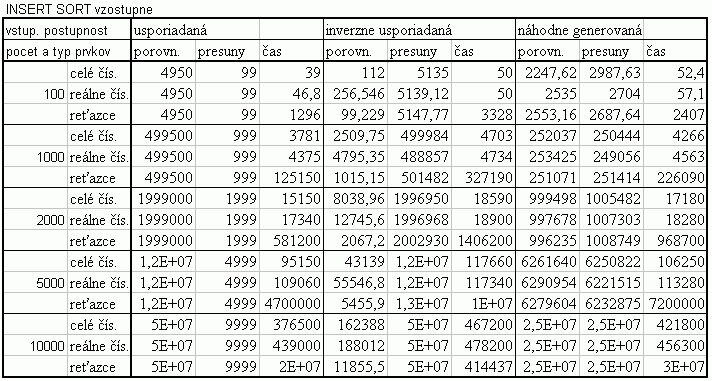
Tabuľka štatistických hodnôt |
 |
| Popis a zložitosť algoritmu |
| Hlavné menu |