 |
Algoritmy usporadúvania |
Shell sort |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Štatistika algoritmu Shell sort |
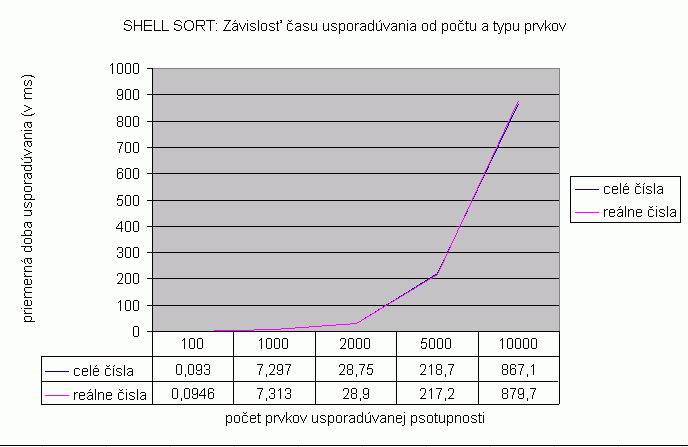
| Na nasledujúcom grafe je znázornená závislosť času usporadúvania vstupnej náhodne generovanej postupnosti od počtu a typu prvkov usporadúvanej postupnosti pre algoritmus Shell sort. Prvky sú typu celé čísla a reálne čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 100 opakovaní, pri 5 000 prvkoch 100 opakovaní a pri 10 000 prvkoch bolo spravených 10 opakovaní. V grafe je vidieť, že krivky znázorňujúce usporadúvanie celých a reálnych čísel sa prakticky prekrývajú. Najväčší rozdiel 12,6 je pri usporiadaní postupnosti s 10 000 prvkami. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu string je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Keďže rozdiel priemerných hodnôt času usporadúvania celých či reálnych čísel a reťazcov je veľký, graf zostrojený z týchto hodnôt nebol dostatočne názorný pre porovnanie času usporadúvania celých a reálnych čísel, preto sú hodnoty času usporadúvania reťazcov zobrazené len v tabuľke. |
 |
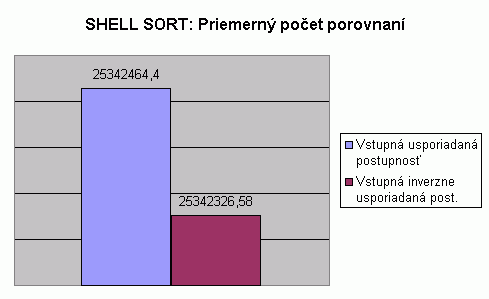
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Shell sort. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti je vyšší než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerné hodnoty počtu porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti sú takisto vyššie než hodnoty pre usporadúvanie vstupnej náhodne vygenerovanej postupnosti. Avšak i napriek tomu môžeme vidieť, že hodnoty pre usporadúvanie ľubovolnej vstupnej postupnosti sú v priemere porovnateľné. Prečo je priemerný počet porovnaní pri usporadúvaní ľubovolnej vstupnej postupnosti porovnateľný? Aj napriek tomu, že Shell sort využíva pri usporadúvaní skupín algoritmus Insert sort, nemožno rátať s výhodou nízkeho počtu porovnaní pri usporadúvaní vstupnej inverzne usporiadanej postupnosti, pretože tým že Shell sort vytvára skupiny s istým krokom, samotná skupina neobsahuje vždy prvky inverzne usporiadané, aj keď vstupná postupnosť je usporiadaná inverzne. V tomto prípade je výhodou oproti algoritmu Insert sort menší počet presunov pri Shell sort. |
 |
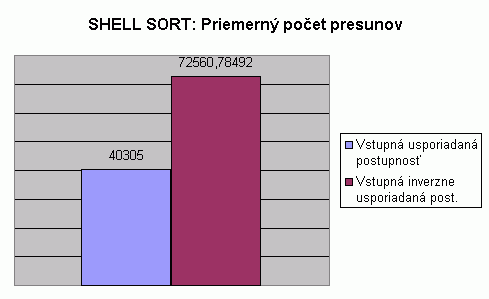
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Shell sort. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerný počet presunov pre usporiadanie vstupnej usporiadanej postupnosti nie je nulový, avšak je približne o polovicu nižší než pri usporiadaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerný počet presunov pre usporiadanie vstupnej náhodnej postupnosti je vyšší než pre usporiadanie vstupnej inverzne usporiadanej postupnosti. Prečo nie je priemerný počet presunov pri usporadúvaní vstupnej usporiadanej postupnosti nulový? Keďže algoritmus Shell sort využíva pri usporadúvaní skupín algoritmus Insert sort, je počet presunov a porovnaní závislý i od Insert sortu, a teda ako bolo spomenuté pri Insert sorte ako presun je započítané i kopírovanie vkladaného prvku do dočasnej premennej, pričom počet presunov vkladaného prvku nie je čisto závislý od počtu prvkov usporadúvanej postupnosti, ale tiež závisí na počte skupín, ktoré sa počas usporadúvania uvažujú. (viď príklad vizualizácie pre vstupnú usporiadanú postupnosť) |
 |
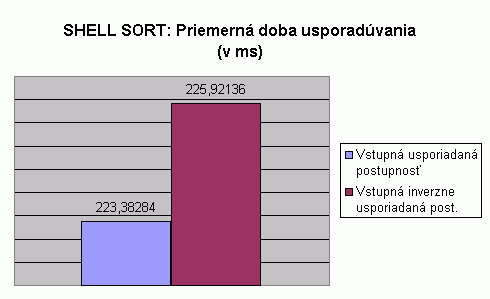
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Shell sort. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerná doba usporadúvania pre usporadúvanie vstupnej usporiadanej postupnosti je nižšia než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. V tabuľke je možné vidieť, že priemerná doba usporadúvania je najvyššia pri usporadúvaní vstupnej náhodne generovanej postupnosti, avšak priemerné hodnoty doby usporadúvania vstupnej inverzne usporiadanej postupnosti a vstupnej náhodne vygenerovanej postupnosti sú porovnateľné, preto možno povedať, že Shell sort je vhodný aj pre usporadúvanie vstupnej inverzne usporiadanej postupnosti. |
 |
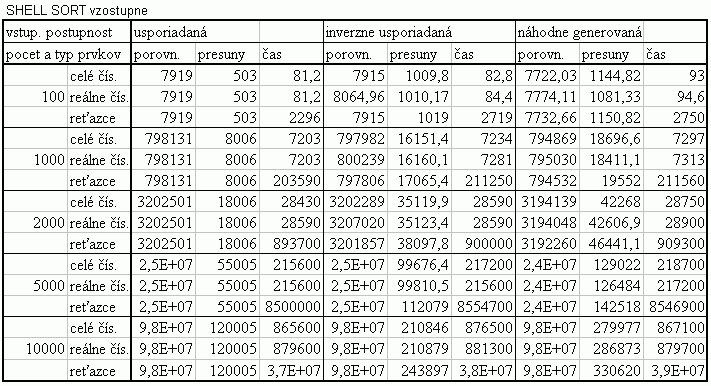
Tabuľka štatistických hodnôt |
 |
| Popis a zložitosť algoritmu |
| Hlavné menu |