 |
Algoritmy usporadúvania |
Merge sort |
| Popis a zložitosť algoritmu |
| Hlavné menu |
Štatistika algoritmu Merge sort |
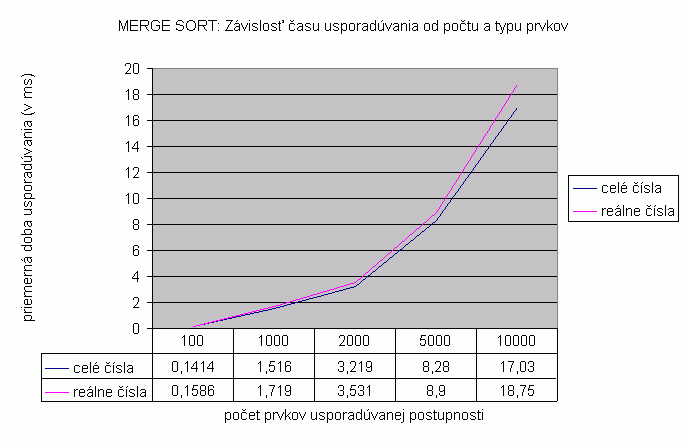
| Na nasledujúcom grafe je znázornená závislosť času usporadúvania vstupnej náhodne generovanej postupnosti od počtu a typu prvkov usporadúvanej postupnosti pre algoritmus Merge sort. Prvky sú typu celé čísla a reálne čísla, čas je udaný v milisekundách. Namerané hodnoty zobrazené v grafe a aj v nižšie uvedenej tabuľke predstavujú priemer z viacerých meraní. Počet opakovaní pri usporadúvaní postupnosti so 100 prvkami bol 10 000, pri 1 000 prvkoch 1 000 opakovaní, pri 2 000 prvkoch 1000 opakovaní, pri 5 000 prvkoch 100 opakovaní a pri 10 000 prvkoch bolo spravených 10 opakovaní. V grafe je rozdiel v priemernej dobe usporadúvania celých a reálnych čísel zreteľne vidieť už pri postupnosti s viac ako 100 prvkami. Rozdiel v priemernom čase usporadúvania je pri postupnosti s 1 000 prvkami 0,203 milisekúnd, pri postupnosti s 10 000 prvkami dosahuje rozdiel najväčšiu hodnotu 1,72 milisekúnd. Priemerné hodnoty času usporadúvania pre usporadúvanie postupnosti prvkov typu string je možné vidieť v tabuľke zobrazenej nižšie. Tieto hodnoty sú takisto priemerné hodnoty z viacerých meraní. Keďže rozdiel priemerných hodnôt času usporadúvania celých či reálnych čísel a reťazcov je veľký, graf zostrojený z týchto hodnôt nebol dostatočne názorný pre porovnanie času usporadúvania celých a reálnych čísel, preto sú hodnoty času usporadúvania reťazcov zobrazené len v tabuľke. |
 |
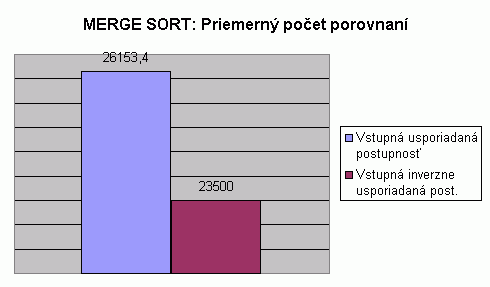
| Na nasledujúcom grafe je znázornené porovnanie počtu porovnaní pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Merge sort. Hodnoty v grafe predstavujú priemer z počtu porovnaní pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu porovnaní pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané aj pri predchádzajúcom grafe. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V nasledujúcom grafe vidíme, že priemerný počet porovnaní pre usporadúvanie vstupnej usporiadanej postupnosti je vyšší než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti. Avšak i napriek tomu môžeme vidieť, že tieto hodnoty sú v priemere porovnateľné. Prečo je priemerný počet porovnaní pri vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti porovnateľný? Merge sort zlučuje dve pomocné usporiadané postupnosti do výslednej usporiadanej postupnosti. V prípade vstupnej inverzne usporiadanej alebo usporiadanej postupnosti sú všetky prvky jednej pomocnej postupnosti vždy menšie (príp. rovné) ako prvky druhej pomocnej postupnosti. Počet porovnaní pri zlučovaní je teda rovný počtu prvkov zlučovanej postupnosti s menšími hodnotami prvkov. V zobrazenom grafe je rozdiel v priemernom počte porovnaní rovný 2653. Rozdiel je spôsobený výskytom rovnakých prvkov v zlučovaných postupnostiach. (viď príklad vizualizácie vstupnej usporiadanej postupnosti) |
 |
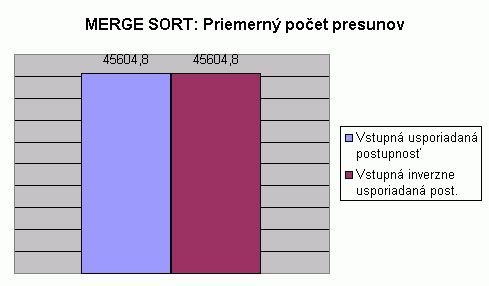
| Na nasledujúcom grafe je znázornené porovnanie počtu presunov pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Merge sort. Hodnoty v grafe predstavujú priemer z počtu presunov pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty počtu presunov pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerný počet presunov pre usporiadanie vstupnej usporiadanej postupnosti je rovný priemernému počtu presunov pri usporiadaní vstupnej inverzne usporiadanej postupnosti. Pri pohľade do tabuľky zistíme, že priemerný počet presunov je pri konkrétnej dĺžke postupnosti rovnaký pre ľubovolnú vstupnú postupnosť. Počet presunov sa zvyšuje pri presúvaní prvkov z pomocných zlučovaných polí do výsledného poľa. Pre postupnosť nemennej dĺžky musíme presunúť vždy rovnaký počet prvkov, preto je počet presunov rovnaký pre akékoľvek usporiadanie vstupnej postupnosti. |
 |
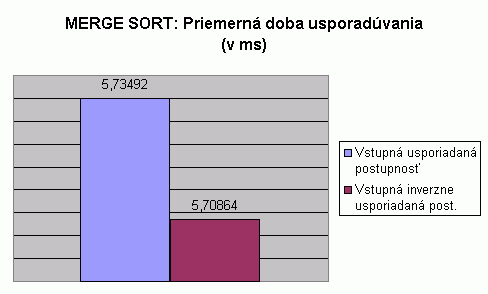
| Na nasledujúcom grafe je znázornené porovnanie priemernej doby usporadúvania pri usporadúvaní vstupnej usporiadanej a vstupnej inverzne usporiadanej postupnosti celých čísel algoritmom Merge sort. Hodnoty v grafe predstavujú priemer z doby usporadúvania pre usporadúvanie postupnosti so 100, 1 000, 2 000, 5 000 a 10 000 prvkami. Hodnoty doby usporadúvania pri usporadúvaní postupnosti s určitým počtom prvkov predstavujú priemery z viacerých meraní, tak ako to bolo popísané pri prvom grafe na tejto stránke. V tabuľke je možné nájsť priemerné hodnoty z meraní usporadúvania rôznych typov prvkov, rôzneho počtu prvkov v usporadúvanej postupnosti a pre rôzne usporiadanie vstupnej postupnosti. V grafe vidíme, že priemerná doba usporadúvania pre usporadúvanie vstupnej usporiadanej postupnosti je vyššia než pri usporadúvaní vstupnej inverzne usporiadanej postupnosti, avšak rozdiel medzi nimi je len 0,029 milisekúnd, čo je spôsobené vyšším počtom porovnaní pri usporadúvaní vstupnej usporiadanej postupnosti. V tabuľke je možné vidieť, že priemerná doba usporadúvania je najvyššia pri usporadúvaní vstupnej náhodne generovanej postupnosti, avšak priemerné hodnoty doby usporadúvania pre ľubovolnú vstupnú postupnosť a pre konkrétny typ prvkov sú porovnateľné, čo je spôsobené najmä rovnakým počtom presunov. |
 |
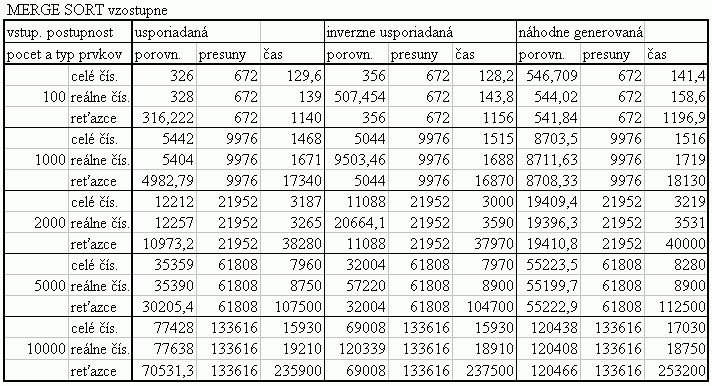
Tabuľka štatistických hodnôt |
 |
| Popis a zložitosť algoritmu |
| Hlavné menu |