Algoritmy pre neusporiadané polia
|
|
Vyhľadávanie oboch extrémov súčasne
|
Popis |
|
V niektorých prípadoch potrebujeme nájsť oba extrémy poľa. V predchádzajúcom prípade sme si ukázali ako nájsť minimum alebo maximum. Teraz si ukážeme, ako nájsť tieto hodnoty naraz a aj výhody, ktoré z takéhoto spoločného vyhľadávania týchto hodnôt pre nás plynú.
|
Vstupy algoritmu |
|
Ako v predchádzajúcom prípade, vstupom tohto algoritmu je iba pole prvkov, v ktorom chceme vyhľadávať. Ďalším vstupom je počet prvkov v poli. Ak je pole ukončené ukončovacím znakom, nie je tento ďalší vstup potrebný a algoritmus po nájdení ukončovacieho znaku hľadanie extrémov ukončí. Zadanie počtu prvkov je ale z hľadiska fungovania algoritmu efektívnejšie a preto sa budeme zaoberať práve týmto prípadom.
|
Princíp činnosti |
|
Na začiatku vezme algoritmus prvé dva prvky poľa a ten väčší označí za maximum a menší za minimum. Ďalej potom algoritmus vždy porovnáva naraz nasledujúce dva prvky uložené vo vstupnom poli za sebou. Ten väčší prvok z dvojice potom porovná s maximom a menší s minimom. V prípade nájdenia nového maxima alebo minima si nové hodnoty zaznamená a pokračuje v prehľadávaní poľa až po jeho koniec. Pri prehľadávaní môžu na konci poľa vzniknúť dve situácie. Ak je počet prvkov párny, potom sa algoritmus jednoducho ukončí, keď sa dostane na koniec poľa. Ak je počet prvkov nepárny, potom s posledným prvkom poľa je nutné vykonať dve porovnania. Jedno s minimom a jedno s maximom.
|
Výstupy algoritmu |
|
Výstupom algoritmu sú hodnoty hľadaných extrémov alebo indexy týchto extrémnych hodnôt v poli prvkov.
|
Vývojový diagram |
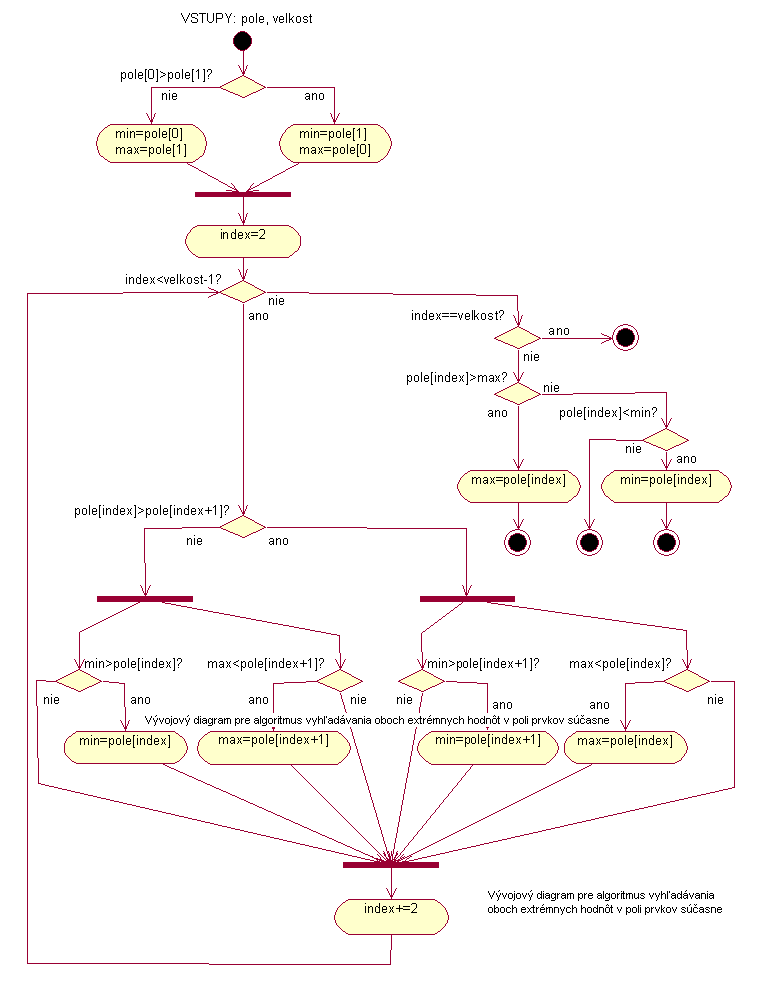 |
Implementácia |
| | //najdenie minimalneho a maximalneho prvku (prvok s najmensou a najvacsou hodnotou)
//v poli "pole" s poctom prvkov "velkost"
//hodnota minima bude po ukonceni funkcie na adrese &hodn_min a
//hodnota maxima na adrese &hodn_max
void najdi_sekv_hodnoty_min_max(int* pole, int velkost, int& hodn_min, int& hodn_max){
if (pole[0] < pole[1]) {
hodn_min=pole[0];
hodn_max=pole[1];
}
else {
hodn_min=pole[1];
hodn_max=pole[0];
}
int index=2;
while (index+1 < velkost) {
if (pole[index] < pole[index+1]) {
if (pole[index] < hodn_min) hodn_min=pole[index];
if (pole[index+1] > hodn_max) hodn_max=pole[index+1];
}
else {
if (pole[index+1] < hodn_min) hodn_min=pole[index+1];
if (pole[index] > hodn_max) hodn_max=pole[index];
}
index+=2;
}
if (index==velkost) return;
if (pole[index] < hodn_min) {hodn_min=pole[index]; return;}
if (pole[index] > hodn_max) hodn_max=pole[index];
return;
} |
Vizualizácie |
| Príklad |
|
Časová zložitosť |
|
Na začiatku algoritmus vykoná jedno porovnanie a jeho výsledkom bude označenie prvých dvoch prvkov za minimum a maximum (resp. naopak). Potom urobí pre ďalších n-2 prvkov (n-2)/2 porovnaní a potom ďalších (n-2)/2 porovnaní s minimom a (n-2)/2 porovnaní s maximom. Dohromady je to teda 1 + (n-2)/2 + (n-2)/2 + (n-2)/2 = 3*(n-2)/2 + 1 = ((3*n)-4)/2 porovnaní. V prípade, že v poli je nepárny počet prvkov, nerobí s poslednými dvomi prvkami 3 porovnania, ale s posledným prvkom iba porovnania 2. Najprv teda urobí iba jedno porovnanie, potom 3*(n-3)/2 porovnania a s posledným prvkom ešte 2 porovnania. V tomto prípade bude teda počet porovnaní 1 + (n-3)/2 + (n-3)/2 + (n-3)/2 + 2 = 3*(n-3)/2 + 3 = ((3*n)-3)/2. Počet týchto porovnaní môžeme zovšeobecniť na približne 3*n/2. K tomu ešte musíme pripočítať počet porovnaní, ktoré musíme vykonať, aby sme zistili čie nie sme na konci poľa. Keďže porovnávame prvky poľa po dvojiciach, počet týchto porovnaní je n/2. Celkový počet porovnaní tohto algoritmu je približne 3*n/2 + n/2 = 2*n porovnaní.
|
Porovnanie s predchádzajúcimi algoritmami |
|
Ako môžeme vidieť, počet porovnaní sa vždy pohybuje rádovo pri 2*n. V predchádzajúcom algoritme, kde sme hľadali iba minimum alebo maximum bol počet porovnaní tiež rovný 2*n. Časové nároky by mali byť pri hľadaní jedného extrému určite menšie, ale keďže počet porovnaní je rádovo rovnaký, môžeme použiť tento algoritmus a získame tak oba extrémy naraz pri rovnakej rádovej časovej zložitosti.
|
| |
| Grafy, tabuľky a porovnanie s predchádzajúcimi algoritmami |
| |
| |
|

