Porovnanie 4.2. |
Rozptyľové tabuľky s otvoreným rozptyľovaním |
| |
| |
Z nameranýh hodnôt je vidieť, že všetky spôsoby riešenia kolízií sú pre 11-riadkovú tabuľku približne rovnako efektívne. Vysoké zaplnenie tabuľky však spolu so zväčšovaním tabuľky spôsobí, že sa začne prejavovať nevhodné rozptyľovanie niektorých spôsobov riešenia kolízií. Metódy linear probing a displaced linear probing sa začnú najprv mierne odpútavať od ostatných metód a pre najväčšiu testovanú tabuľku sa od ostatných časových charakteristík úplne "odtrhnú". I keď sa zdá metóda quadratic residue časovo najlepšia pre stredne veľké tabuľky, pre tú najväčšiu testovanú sa tiež mierne odpúta od dvoch najefektívnejších metód. Je to spôsobené tým, že metódy nedokážu po kolízií vkladanej hodnoty preklenúť v tabuľke veľkú vzdialenosť a tak sa nedokážu dobre vysporiadať s úplným vyčerpaním voľných riadkov v niektorej oblasti tabuľky. |
 |
| |
11 |
101 |
997 |
10007 |
| linear probing |
0,4510 |
0,7210 |
1,618 |
25,86 |
| displaced linear probing |
0,4040 |
1,008 |
1,470 |
5,836 |
| secondary clustering |
0,4380 |
0,8870 |
0,8990 |
0,8100 |
| quadratic residue |
0,4530 |
0,6430 |
0,8460 |
1,315 |
| double hashing |
0,4580 |
0,7260 |
1,004 |
0,8810 |
|
| |
| |
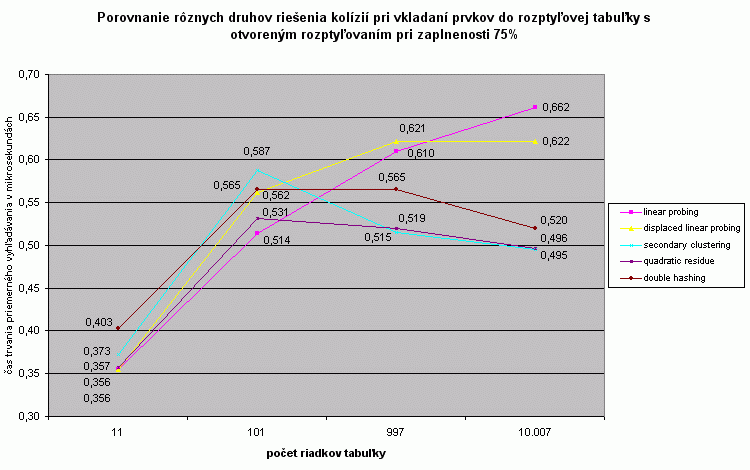
Pri nízkom zaplnení tabuľky sú približne rovnako časovo efektívne 3 metódy. Metódy riešenia kolízií linear probing a displaced linear probing sú stále tými najmenej efektívnymi. |
 |
| |
11 |
101 |
997 |
10007 |
| linear probing |
0,3560 |
0,5140 |
0,6100 |
0,6620 |
| displaced linear probing |
0,3560 |
0,5620 |
0,6210 |
0,6220 |
| secondary clustering |
0,3730 |
0,5870 |
0,5150 |
0,4950 |
| quadratic residue |
0,3570 |
0,5310 |
0,5190 |
0,4960 |
| double hashing |
0,4030 |
0,5650 |
0,5650 |
0,5200 |
|
| |
Toto bola posledná stránka podkapitoly 4.2., venujúcej sa vyhľadávaniu v rozptylových tabuľkách s otvoreným rozptylovaním.
|
| |
|
|

