Porovnanie 5. |
Reťazce |
| |
| |
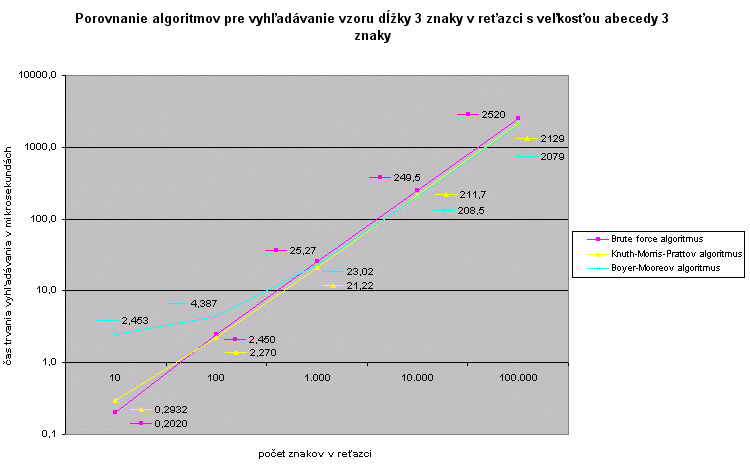
Pre krátke reťace (do 500 znakov) je Boyer-Mooreov algoritmus najpomaľší. Je to z dôvodu časovo náročnej prípravy pomocných tabuliek pred samotným vyhľadávaním. Pre väčšie reťazce sa začína algoritmus brute force odchyľovať od charakteristí ďalších dvoch algoritmov a je výrazne najpomaľší. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| brute force algoritmus |
0,2020 |
2,450 |
25,27 |
249,5 |
2520,0 |
| Knuth-Morris-Prattov algoritmus |
0,2932 |
2,270 |
21,22 |
211,7 |
2129,0 |
| Boyer-Mooreov algoritmus |
2,453 |
4,387 |
23,02 |
208,5 |
2079,0 |
|
| |
| |
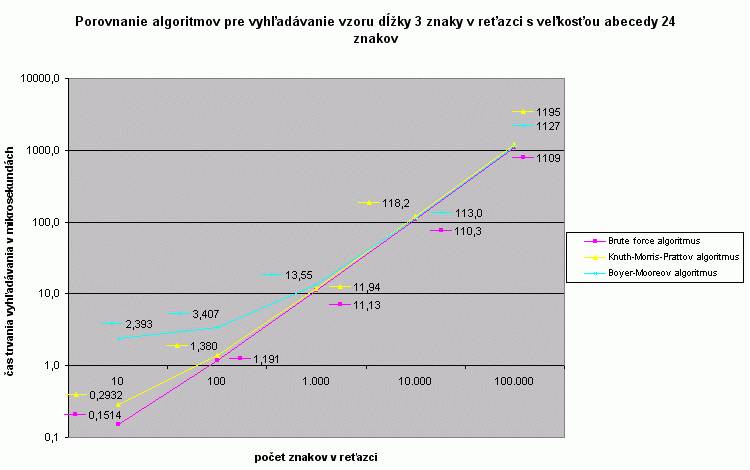
Pre krátke reťace (do 500 znakov) je Boyer-Mooreov algoritmus najpomaľší. Je to z dôvodu časovo náročnej prípravy pomocných tabuliek pred samotným vyhľadávaním. Pre dlhé reťazce sú pri týchto testovacích podmienkach všetky algoritmy približne rovnako efektívne, najlepšie je na tom ale prekvapivo algoritmus brute force. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| brute force algoritmus |
0,1514 |
1,191 |
11,13 |
110,3 |
1109,0 |
| Knuth-Morris-Prattov algoritmus |
0,2837 |
1,380 |
11,94 |
118,2 |
1195,0 |
| Boyer-Mooreov algoritmus |
2,393 |
3,407 |
13,55 |
113,0 |
1127,0 |
|
| |
| |
Príprava pomocných tabuliek oboch dômyselnejších algoritmov ich stojí efektivitu pre krátke reťazce (do 100 znakov). Pre väčšie reťazce sa už ale ríprava začne oplácať a algoritmy nadobúdajú vyššiu efektivitu. V strednej časti vykreslenej časovej závislosti je najefektívnejší algoritmus KMP, pre veľmi dlhé reťazce sa však časovo najefektívnejším stáva BM algoritmus. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| brute force algoritmus |
0,0881 |
2,303 |
24,67 |
250,0 |
2493,0 |
| Knuth-Morris-Prattov algoritmus |
0,4646 |
2,015 |
17,73 |
176,0 |
1769,0 |
| Boyer-Mooreov algoritmus |
2,757 |
3,751 |
17,10 |
141,4 |
1407,0 |
|
| |
| |
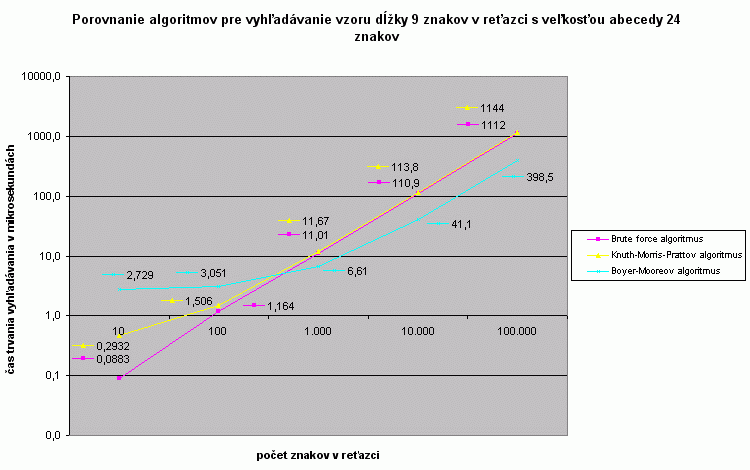
Pre dlhé vzory a mohutné abecedy sa najlepšie prejavuje vykonaná príprava BM algoritmu. Pre krátke reťazce síce nie je práve kvôli nej tento algoritmus najefektívnejší, postupným zväčšovaním prehľadávaného reťazca však získava evidentne pred ostatnými algoritmami náskok. |
 |
| |
10 |
100 |
1.000 |
10.000 |
100.000 |
| brute force algoritmus |
0,0883 |
1,164 |
11,01 |
110,9 |
1111,5 |
| Knuth-Morris-Prattov algoritmus |
0,4647 |
1,506 |
11,67 |
113,8 |
1144,0 |
| Boyer-Mooreov algoritmus |
2,729 |
3,051 |
6,610 |
41,10 |
398,5 |
|
| |
Toto bola posledná stránka kapitoly 5., venujúcej sa vyhľadávaniu zadaného vzoru v reťazci.
|
| |
|
|

