Algoritmy pre reťazce
|
|
Boyer-Mooreov algoritmus
|
Popis |
|
Predchádzajúce algoritmy sa snažili porovnávať znaky vzoru so znakmi reťazca zľava doprava a v reťazci tiež postupovať v tomto smere. Prečo však nezačať porovnávať znaky vzoru a znaky reťazca sprava? V prípade nezhody tak môžeme preskočiť smerom vpravo niekedy omnoho väčšie časti reťazca ako tomu bolo v predchádzajúcom algoritme. Na to, aby sme pri nezhode vedeli správne posunúť vzor v reťazci a opätovne začať porovnávať, budú nám slúžiť dve nasledujúce tabuľky. Prvá z nich bude určovať, o koľko znakov sa môžeme bezpečne posunúť smerom vpravo na základe už načítaných zhodných znakov a druhá nám bude určovať tento istý posun, ale na základe znaku, ktorý sa vo vzore a v reťazci líšil.
|
Vstupy algoritmu |
|
Vstupom algoritmu sú ukazovatele na hľadaný vzor a reťazec, v ktorom vzor budeme vyhľadávať. Opäť je vhodné, ak je vstupom aj počet prvkov vo vzore a v reťazci. Algoritmus si na začiatku ešte vytvorí dve spomínané pomocné tabuľky.
|
Princíp činnosti |
Algoritmus začne s prezeraním reťazca zľava doprava. Samotné znaky vzoru so znakmi reťazca ale porovnáva sprava doľava, čo znamená že porovnáva posledný znak vzoru s aktuálnym znakom v reťazci. Na začiatku je aktuálny znak v reťazci ten, ktorý je uložený na pozícii v reťazci, ktorá odpovedá dĺžke vzoru. V prípade, že algoritmus urobí bezprostredne po sebe počet úspešných porovnaní rovný dĺžke vzoru, skončí úspechom, pretože hľadaný vzor v reťazci našiel. Ak sa pri porovnávaní znaky nezhodujú, použije informácie v tabuľkách na to, aby sa posunul smerom vpravo v reťazci a začal opäť porovnávať posledný znak vzoru s aktuálnym znakom v reťazci. Keďže má algoritmus k dispozícii dve informácie o najmenšom bezpečnom posunutí vpravo, využije tú väčšiu a posunie sa tak najviac vpravo ako je to len pre správne fungovanie algoritmu možné.
Príklad tabuliek pre slovo abracadabra
Tabuľka posunu pre načítané zhodné znaky (úspešne porovnaná postupnosť)
a b r a c a d a b r a
17 16 15 14 13 12 11 13 12 4 1
Tabuľka posunu pre načítaný nezhodný znak (znak v reťazci, ktorý bol iný ako znak vo vzore na odpovedajúcej pozícii)
d['a']=0, d['b']=2, d['c']=6, d['d']=4, d['r']=1,
Pri načítaní iného znaku sa algoritmus posunie vždy o 11 znakov vpravo (d['e']=11, d['f']=11, ...).
|
Výstupy algoritmu |
|
Podobne ako v predchádzajúcich prípadoch je výstupom algoritmu index začiatku vzoru nájdeného v reťazci. Keďže v tomto prípade porovnáva sprava doľava, výstupom je priamo index, pri ktorom spravil posledné úspešné porovnanie a počet úspešných porovnaní sa rovná dĺžke vzoru. V prípade, že sa má posunúť po neúspešnom porovnaní na pozíciu, ktorá sa nachádza až za koncom vstupného reťazca, algoritmus sa končí neúspechom a vzor sa teda v reťazci nenachádza.
|
Vývojový diagram |
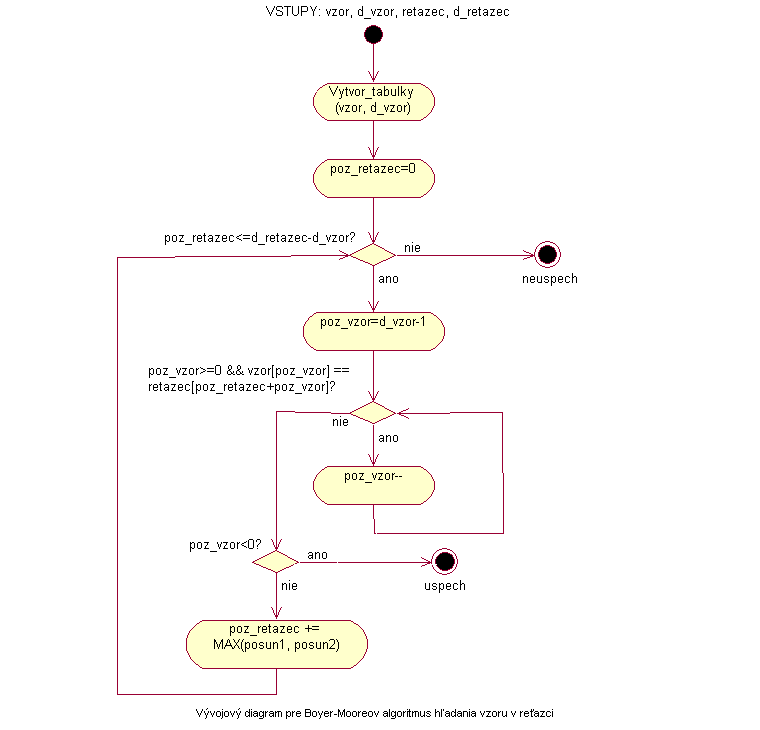 |
Implementácia |
| | //Boyer-Mooreov algoritmus vyhladavania zadaneho vzoru "vzor" s poctom znakov "dlzka_v"
//v retazci "retazec" s poctom znakov "dlzka_r"
//funkcia vracia index prveho znaku najdeneho vzoru v retazci
//(v pripade neuspechu vyhladavania vracia -1)
int najdi_BM(char *vzor, int dlzka_v, char* retazec, int dlzka_r) {
int postupnost[MAX_DLZKA_VZORU];
int vyskyt[MAX_VELKOST_ABECEDY];
pre_postupnost(vzor, dlzka_v, postupnost);
pre_vyskyt(vzor, dlzka_v, vyskyt);
int j = 0;
while (j <= dlzka_r - dlzka_v) {
for (int i = dlzka_v - 1; i >= 0 && vzor[i] == retazec[i + j]; i--);
if (i < 0) {
return j;
//j += postupnost[0];
}
else if (postupnost[i] >= vyskyt[retazec[i + j]] - dlzka_v + 1 + i)
j+=postupnost[i];
else j+=vyskyt[retazec[i + j]] - dlzka_v + 1 + i;
}
return -1;
} |
| Úplná implementácia |
Vizualizácie |
| Príklad 1 |
|
| Príklad 2 |
|
| Priklad 3 |
|
Časová zložitosť |
|
Časová zložitosť sa tento krát skladá z troch časových zložitostí. Najprv treba vypočítať hodnoty oboch tabuliek a až potom dôjde k samotnému vyhľadávaniu. Podľa [7] je časová zložitosť vytvorenia prvej tabuľky O(m) a časová zložitosť vytvorenia druhej je O(m+c). Podľa [11] je pri veľkom počte znakov abecedy priemerná časová zložitosť samotného vyhľadávania približne rovná najlepšiemu prípadu a to je rádovo n/m.
|
Porovnanie s predchádzajúcimi algoritmami |
|
Tento algoritmus je jedným z najrýchlejších používaných algoritmoch pre vyhľadávanie vzoru v reťazci. Je to zabezpečené najmä spôsobom, akým vzor v reťazci vyhľadáva. Oproti predchádzajúcemu algoritmu však potrebuje viac pamäťového priestoru. Je to z dôvodu tvorby tabuľky posunu pre načítaný nezhodný znak so znakom vo vzore. Nároky na pamäťové miesto sú podľa [7] m pre prvú tabuľku a c pre druhú tabuľku.
|
| |
| Grafy, tabuľky a porovnanie s predchádzajúcimi algoritmami |
| |
| |
|

