Mária Bieliková > Knižné publikácie > Funkcionálne a logické programovanie

Príklady funkcionálnych a logických programov

PRÍKLADY Z KNIHY
- Riešenia vybraných príkladov
LISP
- Riešené jednoduché príklady z lispu
- Otázky a odpovede
PROLOG
- Riešené jednoduché príklady z lispu a prologu
- Otázky a odpovede

Riešenia príkladov na overenie:

v lispe (.lsp)
v prologu (.pl)

Text nižšie vo formáte PDF.

Riešenie 1-2:

Výraz a * b + 3 * c znázorníme stromom: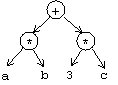

Vyhodnotenie 1: a, a*b, 3*c, a*b+3*c
Vyhodnotenie 2: 3*c, a, a*b, a*b+3*c
Poznámka: Neuvažujeme komutatívnosť operátorov.

Riešenie 1-3:: Záleží na poradí vyhodnotenia podvýrazov, ak pred vyhodnotením výrazu má globálna premenná c hodnotu rôznu od 2.

Riešenie 1-4:

2 * y - (4 * z + x) º -(*(2, y), +(*(4, z), x))

Riešenie 1-5:

and :: (bool x bool) -> bool

and(pravda, nepravda) = nepravda
and(nepravda, pravda) = nepravda
and(nepravda, nepravda) = nepravda
and(pravda, pravda) = pravda

Riešenie 1-6:

faktorial :: int -> int

faktorial(n) = 1, ak n = 0
= n*faktorial(n-1), ak n > 0

faktorial(3) = 1, ak 3 = 0
3*faktorial(3-1), ak 3 > 0

= 3*faktorial(2)

= 3*1, ak 2 = 0
3*2*faktorial(2-1), ak 2 > 0

= 6*faktorial(1)

= 6*1, ak 1 = 0
6*1*faktorial(1-1), ak 1 > 0

= 6*faktorial(0)

= 6*1, ak 0 = 0
6*0*faktorial(0-1), ak 0 > 0

= 6>

Riešenie 1-7:

faktorial(n) = 1, ak n = 0
= n*faktorial(n-1), ak n > 0
¹ m, kde m Î N, ak n < 0

Riešenie 2-1:

CISLO ; atóm (symbol)

(TOTO JE ZOZNAM) ; zoznam

(A B ((1) ) ; nič - nesprávne zátvorky

)( ; nič - nesprávne zátvorky

125 ; atóm (číslo)

T ; atóm (symbol)

((A() ; nič - nesprávne zátvorky

(1 (2 ((3) 4)) 5) ; zoznam

AB( ; nič - nesprávne zátvorky

Riešenie 2-2:

* (FIRST '(A B))
A

* (REST '(A B C))
(B C)

* (FIRST '((A B) (C D)) )
(A B)

* (REST '((A B) (C D)) )
((C D))

* (FIRST (REST '((A B) (C D)) ))
(C D)

* (REST (FIRST '((A B) (C D)) ))
(B)

* (FIRST (FIRST (REST '((A B) (C D)) )))
C

* (REST (FIRST (REST '((A B) (C D)) )))
(D)

Riešenie 2-3:

(FIRST '(A B)) º (CAR '(A B))

(REST '(A B C)) º (CDR '(A B C))

(FIRST '((A B) (C D)) ) º (CAR '((A B) (C D)) )

(REST '((A B) (C D)) ) º (CDR '((A B) (C D)) )

(FIRST (REST '((A B) (C D)) )) º (CADR '((A B) (C D)) )

(REST (FIRST '((A B) (C D)) )) º (CDAR '((A B) (C D)) )

(FIRST (FIRST (REST '((A B) (C D)) ))) º 
(CAADR '((A B) (C D)) )

(REST (FIRST (REST '((A B) (C D)) ))) º 
(CDADR '((A B) (C D)) )

Riešenie 2-4:

(FIRST (REST (REST '(SEAT FELICIA FORD FIAT))))

(FIRST
(FIRST
(FIRST (REST '((SEAT FELICIA) ((FORD)) FIAT)))))

(FIRST
(FIRST
(REST (FIRST '(((SEAT FELICIA) (FORD FIAT)))))))

(FIRST
(FIRST
(REST (REST '(((SEAT)) (FELICIA) (FORD) (FIAT))))))

(FIRST
(REST
(REST (FIRST '(((SEAT) FELICIA FORD) (FIAT))))))

Riešenie 2-5:

(CADDR '(SEAT FELICIA FORD FIAT))

(CAAR (CADR '((SEAT FELICIA) ((FORD)) FIAT)))

(CAAR (CDAR '(((SEAT FELICIA) (FORD FIAT)))))

(CAAR (CDDR '(((SEAT)) (FELICIA) (FORD) (FIAT))))

(CADR (CDAR '(((SEAT) FELICIA FORD) (FIAT))))

Riešenie 2-6:

v zozname je viacnásobný výskyt prvkov dôležitý

Riešenie 2-7:

* (APPEND '(((A) B)) '(1 (((2)) 3) (4)) )
(((A) B) 1 (((2)) 3) (4))

* (LIST '(((A) B)) '(1 (((2)) 3) (4)) )
((((A) B)) (1 (((2)) 3) (4)))

* (CONS '(((A) B)) '(1 (((2)) 3) (4)) )
((((A) B)) 1 (((2)) 3) (4))

* (APPEND '(A B C) NIL)
(A B C)

* (LIST '(A B C) NIL)
((A B C) NIL)

* (CONS '(A B C) NIL)
((A B C))

Riešenie 2-8:

* (FIRST (FIRST (REST (REST '((A B) (C D) (E F)) ))))
E

* (FIRST (FIRST (REST '(REST ((A B) (C D) (E F)) ))))
(A B)

* (FIRST (FIRST '(REST (REST ((A B) (C D) (E F)) ))))
ERROR:
CAR or CDR of non-list object: REST

* (FIRST '(FIRST (REST (REST ((A B) (C D) (E F)) ))))
FIRST

* '(FIRST (FIRST (REST (REST ((A B) (C D) (E F)) ))))
(FIRST (FIRST (REST (REST ((A B) (C D) (E F)) ))))

Riešenie 2-9:

* (CONS (FIRST NIL) (REST NIL))
(NIL)

Riešenie 2-10:

* (+ (/ 8 2) (* 8 2))
20

* (/ (+ 2 (- 3 1)) (* 2 2))
1

Riešenie 2-11:

* (SYMBOLP (CAADR '((((A 1) B) ((2))) ((C 3) D ((4)))) ))
NIL

* (LISTP (CONS '((A 1) B) '((((2) C (3)))) ))
T

* (NULL '(NIL))
NIL ; lebo zoznam má jeden prvok - NIL

* (ATOM NIL)
T

* (NUMBERP (+ (* (- 25 8) (+ 6 3)) (/ 1236 (* 2 2))))
T

Riešenie 2-12:

* (EQ '(A B) '(A B))
NIL

* (EQUAL '(A B) '(A B))
T

Riešenie 2-13:

* (AND (NUMBERP 6) 5 (LIST 3))
(3)

* (OR (NOT (NUMBERP 6)) (CONS '(1) '((2))) 5)
((1) (2))

Riešenie 2-14:

(NOT X) º (COND (X NIL) (T T))

(OR X Y Z) º (COND (X) (Y) (T Z))

(AND P Q R) º (COND ((NOT P) NIL)
((NOT Q) NIL)
( T R))

Riešenie 2-15:

Lambda výraz je:

funkcia

Riešenie 2-16:

(LAMBDA (X) (+ X 5))

* ((LAMBDA (X) (+ X 5)) 2)
7

Riešenie 2-17:

(LAMBDA (F) (- (* (+ F 40) (/ 5 9)) 40) )

(LAMBDA (C) (- (* (+ C 40) (/ 9 5)) 40) )

Riešenie 2-18:

(LAMBDA (ZOZ) (CONS (SECOND ZOZ)
(CONS (FIRST ZOZ)
(REST (REST ZOZ)))) )

Riešenie 2-19:

* (SETQ ZOZ '(A B C))
(A B C)

* (FIRST ZOZ)
A

* (SET (FIRST ZOZ) (+ 2 7))
9 ; hodnota 9 sa priradí symbolu A

* (LIST A)
(9) ; lebo A má hodnotu 9

Riešenie 2-20:

* (SETQ Z '(A B))
(A B)

* (EQ Z Z)
T ; Z je ten istý objekt nezávisle od hodnoty

* (EQ '(A B) '(A B))
NIL

Riešenie 2-21:

* (SETQ PI 3.14)
3.14

* (SYMBOLP PI)
NIL ; lebo hodnota PI je číslo 3.14

* (SYMBOLP 'PI)
T

* (AND (LISTP PI) (SETQ VYSLEDOK 'PRVY-AND))
NIL ; lebo PI nie je zoznam

* VYSLEDOK
ERROR: ; lebo VYSLEDOK nemá hodnotu, pretože
Unbound variable: VYSLEDOK ; druhá forma v AND sa nevyhodnotila

* (AND (NUMBERP PI) (SETQ VYSLEDOK 'DRUHY-AND))
DRUHY-AND

* VYSLEDOK
DRUHY-AND

Riešenie 2-22:

;ROTUJ-VLAVO :: [a] -> [a]
(DEFUN ROTUJ-VLAVO (ZOZ)
(APPEND (REST ZOZ) (LIST (FIRST ZOZ))) )

Riešenie 2-23:

;OHRANICENIE :: (int x int x int) -> int
(DEFUN OHRANICENIE (X MINIMUM MAXIMUM)
(COND ((< X MINIMUM) MINIMUM)
((> X MAXIMUM) MAXIMUM)
( T X) ))

Riešenie 2-24:

;SUSED :: int -> int
(DEFUN SUSED (N)
(COND ((< N 0) (- N 1))
((> N 0) (+ N 1))
( T N) ))

Riešenie 2-25:

;CYKLUS :: nat -> nat
(DEFUN CYKLUS (N)
(COND ((= N 99) 1)
( T (+ N 1)) ))

Poznamenajme, že takto definovaná funkcia CYKLUS pracuje očakávaným spôsobom iba pre čísla z intervalu <1, 99>.

Riešenie 2-26:

;MIN-DVA :: (int x int) -> int
(DEFUN MIN-DVA (X Y)
(COND ((< X Y) X) ; X < Y?
( T Y) )) ; X 3 Y

Riešenie 2-27:

;MAX-TRI :: (int x int x int) -> int
(DEFUN MAX-TRI (X Y Z)
(COND ((AND (< X Y) 
(OR (= Z Y)(< Z Y))) Y)
((AND (< X Z) (< Y Z)) Z)
( T X) ))

Riešenie 2-28:

;OPERACIA :: (int x int x int) -> symb
(DEFUN OPERACIA (A1 A2 VYSLEDOK)
(COND ((= (+ A1 A2) VYSLEDOK) 'PLUS)
((= (- A1 A2) VYSLEDOK) 'MINUS)
((= (* A1 A2) VYSLEDOK) 'KRAT)
((= (/ A1 A2) VYSLEDOK) 'DELENO)
( T NIL) ))

Riešenie 2-29:

(DEFUN OPERACIA-HLAVNA ()
(TERPRI)
(PRINC " Zadaj prvy argument: ")
(SETQ A1 (READ))
(PRINC " Zadaj druhy argument: ")
(SETQ A2 (READ))
(PRINC " Zadaj vysledok: ")
(SETQ VYSLEDOK (READ))
(OPERACIA A1 A2 VYSLEDOK) )

V tomto prípade však po vyhodnotení funkcie OPERACIA-HLAVNA ostanú väzby na hodnoty pre symboly A1, A2 a VYSLEDOK. Druhá alternatíva funkcie OPERACIA-HLAVNA1 tento nedostatok odstraňuje:

(DEFUN OPERACIA-HLAVNA1 ()
(TERPRI)
(OPERACIA (NACITAJ "Zadaj prvy argument : ")
(NACITAJ "Zadaj druhy argument: ")
(NACITAJ "Zadaj vysledok: ") ))

(DEFUN NACITAJ (TEXT)
(PRINC TEXT)
(READ) )

Riešenie 2-30:

;MAX-TRI-HLAVNA :: (a x a x a) -> a
(DEFUN MAX-TRI-HLAVNA (X Y Z)
(COND ((AND (NUMBERP X)(NUMBERP Y)(NUMBERP Z))
(MAX-TRI X Y Z))
( T 'CHYBA) ))

Riešenie 2-31:

Korene x₁ a x₂ kvadratickej rovnice a * x² + b * x + c vypočítame podľa vzťahov: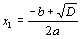

, ,

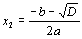kde číslo D = b² – 4ac (diskriminant kvadratickej rovnice). Na základe týchto vzťahov:

ak D > 0, rovnica má dva rôzne reálne korene,
ak D = 0, rovnica má jeden dvojnásobný koreň,
ak D < 0, riešením rovnice sú dve komplexne združené čísla

, .

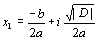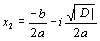Riešenie využíva pomocný argument na výpočet diskriminantu a formu LET na výpočet spoločných podvýrazov:

;KVADER :: (int x int x int) -> (symb,real,real)
(DEFUN KVADER (A B C)
(KVADER-AUX A B C (- (* B B)(* 4 A C))))

(DEFUN KVADER-AUX (A B C D)
(LET ((MINUS-B (- B))
(SQRT-D (SQRT (ABS D)))
(DVE-A (* A 2)) )
(COND ((< D 0)
(LIST 'KOMPLEX 
(/ MINUS-B DVE-A) 
(/ SQRT-D DVE-A)) )
(T (LIST 'REAL 
(/ (+ MINUS-B SQRT-D) DVE-A)
(/ (- MINUS-B SQRT-D) DVE-A)) )) ))

Riešenie 2-32:

;POCITAJ :: (a x a x b) -> int
(DEFUN POCITAJ (LAVY-OPERAND PRAVY-OPERAND OPERATOR)
(EVAL (LIST OPERATOR LAVY-OPERAND PRAVY-OPERAND)) )

Riešenie 3-1:

;SUCIN :: [int] -> int 
(DEFUN SUCIN (ZOZ)
(COND ((NULL ZOZ) 1)
( T (* (FIRST ZOZ) (SUCIN (REST ZOZ)))) ))

Riešenie 3-2:

;MAP-CUBE :: [int] -> [int]
(DEFUN MAP-CUBE (ZOZ)
(COND ((NULL ZOZ) NIL)
( T (CONS (CUBE (FIRST ZOZ))
(MAP-CUBE (REST ZOZ)))) ))

(DEFUN CUBE (N) (* (* N N) N))

Riešenie 3-3:

;VYBER-PARNE :: [a] -> [int]
(DEFUN VYBER-PARNE (ZOZ)
(COND ((NULL ZOZ) NIL)
((AND (NUMBERP (FIRST ZOZ))
(EVENP (FIRST ZOZ)))
(CONS (FIRST ZOZ)
(VYBER-PARNE (REST ZOZ))))
(T (VYBER-PARNE (REST ZOZ))) ))

Riešenie 3-4:

;POCET-PARNYCH :: [a] -> nat
(DEFUN POCET-PARNYCH (ZOZ)
(COND ((NULL ZOZ) 0)
((AND (NUMBERP (FIRST ZOZ))
(EVENP (FIRST ZOZ)))
(+ 1 (POCET-PARNYCH (REST ZOZ))))
(T (POCET-PARNYCH (REST ZOZ))) ))

Riešenie 3-5:

;PRVE-PARNE :: [a] -> int
(DEFUN PRVE-PARNE (ZOZ)
(COND ((NULL ZOZ) NIL)
((AND (NUMBERP (FIRST ZOZ))
(EVENP (FIRST ZOZ)))
(FIRST ZOZ))
(T (PRVE-PARNE (REST ZOZ))) ))

Riešenie 3-6:

;LAST-MY :: [a] -> [a]
(DEFUN LAST-MY (ZOZ)
(COND ((NULL (REST ZOZ)) ZOZ)
( T (LAST-MY (REST ZOZ))) ))

Riešenie 3-8:

;POSTFIX :: (a x [a]) -> [a]
(DEFUN POSTFIX (SV ZOZ)
(COND ((NULL ZOZ) (LIST SV))
( T (CONS (FIRST ZOZ)
(POSTFIX SV (REST ZOZ)))) ))

Riešenie 3-9:

;CISLA :: [a] -> bool
(DEFUN CISLA (ZOZ)
(COND ((NULL ZOZ) T)
((NUMBERP (FIRST ZOZ)) (CISLA (REST ZOZ)))
( T NIL) ))

Riešenie 3-10:

;PARNE :: [a] -> bool
(DEFUN PARNE (ZOZ)
(COND ((NULL ZOZ) T) ; prázdny ZOZ - párny počet prvkov
((NULL (REST ZOZ)) NIL) ; jednoprvkový ZOZ - nepárny počet
(T (PARNE ; rekurzia ..
(REST (REST ZOZ)))) ; .. o dva prvky kratší ZOZ
))

Riešenie 3-11:

;VYRAZ :: [a] -> bool
(DEFUN VYRAZ (SV)
(OR (NUMBERP SV) ; číslo je aritmetický výraz
(AND (LISTP SV) ; zoznam:
(VYRAZ (FIRST SV)) ; prvý prvok je aritmetický výraz
(OPERATOR (SECOND SV)) ; druhý prvok je operátor
(VYRAZ (THIRD SV)) ; tretí prvok je aritmetický výraz
(NULL (CDDDR SV))) ; SV neobsahuje štvrtý prvok
))

;OPERATOR :: symb -> bool
(DEFUN OPERATOR (OP)
(OR (EQ OP '+) (EQ OP '-) (EQ OP '*) (EQ OP '/)) )

Riešenie 3-12:

;MAX-ZOZ :: [a] -> nat
(DEFUN MAX-ZOZ (ZOZ)
(MAX-ZOZ-AUX ZOZ 0))

;MAX-ZOZ-AUX :: ([a] x nat) -> nat
(DEFUN MAX-ZOZ-AUX (ZOZ POCET)
(COND ((NULL ZOZ) POCET)
((ATOM (FIRST ZOZ))
(MAX-ZOZ-AUX (REST ZOZ) POCET))
((< POCET (LENGTH (FIRST ZOZ)))
(MAX-ZOZ-AUX (REST ZOZ)
(LENGTH (FIRST ZOZ))))
( T (MAX-ZOZ-AUX (REST ZOZ) POCET)) ))

Funkcia MAX-ZOZ iba inicializuje funkciu MAX-ZOZ-AUX, ktorá má dva argumenty, nie iba jeden. Druhý argument predstavuje dĺžku najdlhšieho doteraz zisteného podzoznamu.

Nevýhoda tejto definície je v tom, že ak je dĺžka podzoznamu väčšia ako aktuálne najdlhší podzoznam, počíta sa jeho dĺžka dvakrát. Túto nevýhodu možno odstrániť napr. použitím formy LET:

(DEFUN MAX-ZOZ-AUX1 (ZOZ POCET)
(COND ((NULL ZOZ) POCET)
((ATOM (FIRST ZOZ))
(MAX-ZOZ-AUX1 (REST ZOZ) POCET))
((LET
((DLZKA ; lokálna premenná
(LENGTH (FIRST ZOZ)) ; hodnota
)
; môžu nasledovať ďalšie
) ; deklarácie
(< POCET DLZKA) ; forma-1
(MAX-ZOZ-AUX1 (REST ZOZ) ; forma-2
DLZKA) ))
( T (MAX-ZOZ-AUX1 (REST ZOZ) POCET)) ))

Riešenie 3-13:

;MIN :: [int] -> int
(DEFUN MIN (ZOZ)
(COND ((NULL (REST ZOZ)) (FIRST ZOZ)) ; koniec rekurzie
((< (FIRST ZOZ) (SECOND ZOZ)) ; prvý menší ako druhý?
(MIN (CONS (FIRST ZOZ) ; zaraď prvý (menší)
(CDDR ZOZ))) ) ; druhý vynechaj
( T ; druhý menší ako prvý
(MIN (REST ZOZ))) )) ; prvý vynechaj

Podobný postup sa dá použiť aj na alternatívne riešenie cvičenia 3-12. V tomto prípade sa však ešte zvýši počet pokusov o zistenie dĺžky jednotlivých podzoznamov.

Riešenie 3-14:

;ZLUC :: ([int] x [int]) -> [int]
(DEFUN ZLUC (ZOZ1 ZOZ2)
(COND ((NULL ZOZ1) ZOZ2)
((NULL ZOZ2) ZOZ1)
((= (FIRST ZOZ1) (FIRST ZOZ2))
(CONS (FIRST ZOZ1)
(ZLUC (REST ZOZ1) (REST ZOZ2))))
((< (FIRST ZOZ1) (FIRST ZOZ2))
(CONS (FIRST ZOZ1)
(ZLUC (REST ZOZ1) ZOZ2)))
( T (CONS (FIRST ZOZ2)
(ZLUC ZOZ1 (REST ZOZ2)))) ))

Riešenie 3-15:

;PRVYCH-K :: (nat x [a]) -> [a]
(DEFUN PRVYCH-K (K ZOZ)
(COND ((NULL ZOZ) NIL)
((= K 0) NIL)
( T (CONS (FIRST ZOZ)
(PRVYCH-K (- K 1) (REST ZOZ)))) ))

Prvá alternatíva vo forme COND je dôležitá iba v prípade, ak číslo K je väčšie ako počet prvkov zoznamu ZOZ.

Riešenie 3-16:

;BEZ-PRVYCH-K :: (nat x [a]) -> [a]
(DEFUN BEZ-PRVYCH-K (K ZOZ)
(COND ((= K 0) ZOZ)
( T (BEZ-PRVYCH-K (- K 1) (REST ZOZ))) ))

Ako sa bude správať funkcia BEZ-PRVYCH-K v prípade, ak číslo K je väčšie ako počet prvkov zoznamu?

Riešenie 3-17:

;ZAMEN :: (a x a x [a]) -> [a]
(DEFUN ZAMEN (SV1 SV2 ZOZ)
(COND ((NULL ZOZ) NIL)
((EQUAL SV1 (FIRST ZOZ))
(CONS SV2
(ZAMEN SV1 SV2 (REST ZOZ))))
( T (CONS (FIRST ZOZ)
(ZAMEN SV1 SV2 (REST ZOZ)))) ))

Riešenie 3-18:

;V-CISLA :: [a] -> bool
(DEFUN V-CISLA (SV)
(COND ((NULL SV) T)
((NUMBERP SV) T)
((ATOM SV) NIL)
( T (AND (V-CISLA (FIRST SV))
(V-CISLA (REST SV)))) ))

Riešenie 3-19:

;V-POCET-PARNYCH :: [a] -> nat
(DEFUN V-POCET-PARNYCH (SV)
(COND ((AND (NUMBERP SV) (EVENP SV)) 1)
((ATOM SV) 0)
( T (+ (V-POCET-PARNYCH (FIRST SV))
(V-POCET-PARNYCH (REST SV)))) ))

Alternatívu ((NULL SV) 0) netreba, pretože ((ATOM SV) 0) zahŕňa aj prázdny zoznam.

Riešenie 3-20:

;V-PRVE-PARNE :: [a] -> int
(DEFUN V-PRVE-PARNE (SV)
(COND ((AND (NUMBERP SV) (EVENP SV)) SV)
((ATOM SV) NIL)
(T (OR (V-PRVE-PARNE (FIRST SV))
(V-PRVE-PARNE (REST SV)))) ))

Riešenie 3-21:

;V-VYBER-PARNE :: [a] -> [b]
(DEFUN V-VYBER-PARNE (ZOZ)
(COND ((NULL ZOZ) NIL)
((AND (NUMBERP (FIRST ZOZ))
(EVENP (FIRST ZOZ)))
(CONS (FIRST ZOZ)
(V-VYBER-PARNE (REST ZOZ))))
((ATOM (FIRST ZOZ))
(V-VYBER-PARNE (REST ZOZ)))
(T (CONS (V-VYBER-PARNE (FIRST ZOZ))
(V-VYBER-PARNE (REST ZOZ)))) ))

Riešenie 3-22:

;V-ZAMEN :: (a x b x [g]) -> [d]
(DEFUN V-ZAMEN (SV1 SV2 ZOZ)
(COND ((NULL ZOZ) NIL)
((EQUAL SV1 ZOZ) SV2)
((ATOM ZOZ) ZOZ)
( T (CONS (V-ZAMEN SV1 SV2 (FIRST ZOZ))
(V-ZAMEN SV1 SV2 (REST ZOZ)))) ))

Riešenie 3-23:

;ZATVORKY :: [a] -> [b]
(DEFUN ZATVORKY (X)
(COND ((NULL X) NIL)
((ATOM X) (LIST X))
( T (APPEND (ZATVORKY (FIRST X))
(ZATVORKY (REST X)))) ))

Riešenie 3-24:: Funkcia HADAJ vráti kópiu daného s-výrazu a funkcia NEVIEM počíta najväčšiu hĺbku vnoreného zoznamu.

Riešenie 3-25:

;SUCIN2 :: [int] -> int
(DEFUN SUCIN2 (ZOZ)
(SUCIN-AUX ZOZ 1))

;SUCIN-AUX :: ([int] x int) -> int
(DEFUN SUCIN-AUX (ZOZ SUCIN)
(COND ((NULL ZOZ) SUCIN)
( T (SUCIN-AUX (REST ZOZ)
(* SUCIN (FIRST ZOZ)))) ))

Riešenie 3-26:

;MAP-CUBE2 :: [int] -> [int]
(DEFUN MAP-CUBE2 (ZOZ)
(MAP-CUBE-AUX ZOZ NIL))

;MAP-CUBE-AUX :: ([int] x [int]) -> [int]
(DEFUN MAP-CUBE-AUX (ZOZ MAP-ZOZ)
(COND ((NULL ZOZ) MAP-ZOZ)
(T (MAP-CUBE-AUX (REST ZOZ)
(APPEND MAP-ZOZ
(LIST (CUBE (FIRST ZOZ)))) ))

Riešenie 3-27:

;POCET-PARNYCH2 :: [a] -> nat
(DEFUN POCET-PARNYCH2 (ZOZ)
(POCET-PARNYCH-AUX ZOZ 0))

;POCET-PARNYCH-AUX :: ([a] x nat) -> nat
(DEFUN POCET-PARNYCH-AUX (ZOZ POCET)
(COND ((NULL ZOZ) POCET)
((AND (NUMBERP (FIRST ZOZ))
(EVENP (FIRST ZOZ)))
(POCET-PARNYCH-AUX (REST ZOZ)
(+ 1 POCET)))
( T (POCET-PARNYCH-AUX (REST ZOZ) POCET)) ))

Riešenie 3-28:

;V-POCET-PARNYCH2 :: [a] -> nat
(DEFUN V-POCET-PARNYCH2 (SV)
(V-POCET-AUX SV NIL 0))

;V-POCET-AUX :: ([a] x [a] x nat) -> nat
(DEFUN V-POCET-AUX (SV RSV AUX)
(COND ((AND (NULL SV)(NULL RSV)) ;prešli sme celý zoznam
AUX)
((NULL SV) ;koniec FIRST časti
(V-POCET-AUX (FIRST RSV) ;spracujeme zvyšky...
(REST RSV) ;a zásobník skrátime
AUX ))
((AND (NUMBER SV)(EVENP SV)) ;párne číslo
(V-POCET-AUX NIL
RSV
(+ 1 AUX) )) ;pripočítame do AUX
((ATOM SV) ;ostatné atómy...
(V-POCET-AUX NIL
RSV
AUX )) ;...nezapočítame
(T ;SV je zoznam...
(V-POCET-AUX (FIRST SV) ;...pokračujeme s FIRST
(CONS (REST SV) RSV) ;a REST odložíme
AUX ))
))

Riešenie 3-29:

;ZLUC2 :: ([int] x [int]) -> [int]
(DEFUN ZLUC2 (ZOZ1 ZOZ2)
(ZLUC-AUX ZOZ1 ZOZ2 NIL))

;ZLUC-AUX :: ([int] x [int] x [int]) -> [int]
(DEFUN ZLUC-AUX (ZOZ1 ZOZ2 VYSLEDOK)
(COND ((NULL ZOZ1) (APPEND VYSLEDOK ZOZ2))
((NULL ZOZ2) (APPEND VYSLEDOK ZOZ1))
((= (FIRST ZOZ1) (FIRST ZOZ2))
(ZLUC-AUX (REST ZOZ1) (REST ZOZ2)
(APPEND VYSLEDOK
(LIST (FIRST ZOZ1)) )))
((< (FIRST ZOZ1) (FIRST ZOZ2))
(ZLUC-AUX (REST ZOZ1) ZOZ2
(APPEND VYSLEDOK
(LIST (FIRST ZOZ1)) )))
( T (ZLUC-AUX ZOZ1 (REST ZOZ2)
(APPEND VYSLEDOK
(LIST (FIRST ZOZ2)) ))) ))

Riešenie 3-30:

;ANO-NIE :: string -> bool
(DEFUN ANO-NIE (TEXT)
(PROG (ODPOVED)
(TERPRI)
ZAC (PRINC TEXT) (PRINC " A/N ? ")
(SETQ ODPOVED (READ))
(COND ((EQ ODPOVED 'A) (RETURN T))
((EQ ODPOVED 'N) (RETURN NIL))
( T (GO ZAC))) ))

Riešenie 3-31:

;ANO-NIE2 :: string -> bool
(DEFUN ANO-NIE2 (TEXT)
(PRINC TEXT) (PRINC " A/N ? ")
(ODPOVED (READ) TEXT))

;ODPOVED :: (a x string) -> bool
(DEFUN ODPOVED (SV TEXT)
(COND ((EQ SV 'A) T)
((EQ SV 'N) NIL)
( T (ANO-NIE2 TEXT)) ))

Riešenie 3-32:

;EVERY :: ((a -> bool) x [a]) -> bool
(DEFUN EVERY (FN ZOZ)
(COND ((NULL ZOZ) T)
((FUNCALL FN (FIRST ZOZ))
(EVERY FN (REST ZOZ)))
(T NIL) ))

Riešenie 3-33:

;NESTED-REMOVE-IF :: ((a -> bool) x [b]) -> [b] 
(DEFUN NESTED-REMOVE-IF (FN ZOZ)
(COND ((NULL ZOZ) NIL)
((FUNCALL FN (FIRST ZOZ))
(NESTED-REMOVE-IF FN (REST ZOZ)))
((ATOM (FIRST ZOZ))
(CONS (FIRST ZOZ)
(NESTED-REMOVE-IF FN (REST ZOZ))))
( T (CONS (NESTED-REMOVE-IF FN (FIRST ZOZ))
(NESTED-REMOVE-IF FN (REST ZOZ)))) ))

Riešenie 3-34:

;NESTED-MAP-IF :: ((a -> b) x (a -> bool) x [g]) -> [d]
(DEFUN NESTED-MAP-IF (FN-MAP FN-IF SV)
(COND ((FUNCALL FN-IF SV) (FUNCALL FN-MAP SV))
((ATOM SV) SV)
(T (CONS (NESTED-MAP-IF FN-MAP FN-IF (FIRST SV))
(NESTED-MAP-IF FN-MAP FN-IF (REST SV))
))
))

Riešenie 3-35:

;OBSAHUJE :: ((a -> bool) x [b]) -> bool
(DEFUN OBSAHUJE (FN SV)
(COND ((FUNCALL FN SV) T)
((ATOM SV) NIL)
(T (OR (OBSAHUJE FN (FIRST SV))
(OBSAHUJE FN (REST SV)))) ))

Riešenie 3-36:

(REMOVE-IF
#'(LAMBDA (X) (AND (NUMBERP X)(EVENP X)(> X 6)))
'(5 6 7 8 9))

Riešenie 3-37:

;VYBER-ZAPORNE :: [a] -> [int]
(DEFUN VYBER-ZAPORNE (ZOZ)
(REMOVE-IF-NOT #'(LAMBDA (X) (< X 0)) ZOZ))

Riešenie 3-38:

;V-POCET-PARNYCH3 :: [a] -> nat
(DEFUN V-POCET-PARNYCH3 (SV)
(COND ((AND (NUMBERP SV) (EVENP SV)) 1)
((ATOM SV) 0)
( T (APPLY '+ (MAPCAR #'V-POCET-PARNYCH3 SV))) ))

Riešenie 4-1:

Vo výpisoch uvádzame iba tie premenné, ktoré nás zaujímajú z hľadiska zadania cvičenia.

?- vedúci(V, nadutý), vedúci(V, klebetná).
V = usilovná -> ;
no

?- vedúci(V, klebetná), vedúci(V, P). % V nezaujímavé
P = nadutý -> ;
P = simulantový -> ;
P = klebetná -> ;
no

```
?- vedúci(rozkošná, P).
no
```

Riešenie 4-2:

```
?- rodič(semidrag, svätopluk).
yes
```
```
?- rodič(mojmír, rastislav).
no
```

?- rodič(R, svätopluk).
R = rodana -> ;
R = semidrag -> ;
no

?- rodič(semidrag, D).
D = svätopluk -> ;
D = semižizeň -> ;
no

?- rodič(S, D), rodič(D, svätopluk).
S = všeslav ->;
no

?- rodič(samoslav, D), rodič(D, V). % D nezaujímavé
V = rastislav -> ;
V = semidrag -> ;
no

?- rodič(S, D), rodič(D, V). % D nezaujímavé
S = samoslav, V = rastislav -> ;
S = samoslav, V = semidrag -> ;
S = všeslav, V = svätopluk -> ;
S = všeslav, V = semižizeň -> ;
no

?- rodič(R, svätopluk), rodič(R, semižizeň).
R = rodana -> ;
R = semidrag -> ;
no

Riešenie 4-3:

?- a(X,Y), b(X,Y).
X = 3, Y = 2 -> ;
X = 4, Y = 4 -> ;
no

?- a(X,Y), b(Y,X).
X = 2, Y = 1 -> ;
X = 3, Y = 2 -> ;
X = 4, Y = 4 -> ;
no

?- a(X,Y), b(X,Y), a(Y,Y).
X = 4, Y = 4 -> ;
no

Riešenie 4-4:

Kto (X) píše báseň a aj list?
Koho (X) má rád Peter?
V ktorej európskej krajine (X) sa hovorí nemecky?

Riešenie 4-5:

dôležitý(ZAMESTNANEC) :-
vedúci(ZAMESTNANEC, PODRIADENÝ).

alebo

dôležitý(ZAMESTNANEC) :-
vedúci(ZAMESTNANEC, _).

Riešenie 4-6:

dieťa(DIEŤA, RODIČ) :- 
rodič(RODIČ, DIEŤA).

matka(MATKA, DIEŤA) :-
rodič(MATKA, DIEŤA),
žena(MATKA).

syn(SYN, RODIČ) :- 
rodič(RODIČ, SYN), muž(SYN).

starý_rodič(STARKÝ, VNÚČA) :-
rodič(STARKÝ, DIEŤA),
rodič(DIEŤA, VNÚČA).

brat(BRAT, SÚRODENEC) :-
rodič(RODIČ, BRAT),
rodič(RODIČ, SÚRODENEC),
muž(BRAT),
rôzne(BRAT, SÚRODENEC).

strýko(STRÝKO, DIEŤA) :-
rodič(RODIČ, DIEŤA),
muž(RODIČ),
brat(STRÝKO, RODIČ).

predok(PREDOK, POTOMOK) :- 
rodič(PREDOK, POTOMOK).
predok(PREDOK, POTOMOK) :-
rodič(PREDOK, X),
predok(X, POTOMOK).

Riešenie 4-7:

"Pre všetky S a D, S je stará mama D, ak:
1. S je žena a
2. existuje R také, že S je rodič R a R je rodič D"
Iná alternatíva:

"Pre všetky S, D a R, S je stará mama D, ak:
1. S je žena a
2. S je rodič R a
3. R je rodič D"
Pre všetky X, Peter má rád X, ak:
1. X je hračka a
2. Peter sa hrá s X"

Riešenie 4-8:

šikovný(X):- % 1
študuje(X, Y), 
softvérové_inžinierstvo(Y). 
študuje(peter, flp). % 2
študuje(jana, ma1). % 3
softvérové_inžinierstvo(flp). % 4
matematika(ma1). % 5

fakty: klauzuly 2, 3, 4, 5
pravidlá: klauzula 1
premenné: X, Y
atómy: peter, flp, jana, ma1
relácie: šikovný, študuje, softvérové_inžinierstvo, matematika
```
?- šikovný(X).
X = peter -> ;
no
```

Logický význam odpovede možno opísať takto:

"X je šikovný, ak študuje predmet softvérového inžinierstva Y. Peter študuje FLP a FLP je predmet softvérového inžinierstva, preto Peter je šikovný".

Riešenie 4-9:

kategória(citrokola, nealko).
kategória(víno, ľahký_alkohol).
kategória(pivo, ľahký_alkohol).
kategória(whisky, tvrdý_alkohol).

vek(martin, 25).
vek(pavol, 15).
vek(júlia, 20).
vek(mária, 21).

predaj(OSOBA, NÁPOJ) :-
kategória(NÁPOJ, tvrdý_alkohol),
vek(OSOBA, VEK), VEK >= 21.
predaj(OSOBA, NÁPOJ) :-
kategória(NÁPOJ, ľahký_alkohol),
vek(OSOBA, VEK), VEK >= 18.
predaj(OSOBA, NÁPOJ) :-
kategória(NÁPOJ, nealko).

Test programu:

```
?- predaj(martin, whisky).
yes
```

?- predaj(júlia, NÁPOJ).
NÁPOJ = citrokola ->;
NÁPOJ = víno ->;
NÁPOJ = pivo ->;
no

?- predaj(OSOBA, víno).
OSOBA = martin -> ;
OSOBA = júlia -> ;
OSOBA = mária -> ;
no

Riešenie 4-10:

cesta(X, Y) :- priama_cesta(X, Y).
cesta(X, Y) :- priama_cesta(X, Z), cesta(Z, Y).

Riešenie 4-11:

deň_v_týždni(pondelok).
deň_v_týždni(utorok).
deň_v_týždni(streda).
deň_v_týždni(štvrtok).
deň_v_týždni(piatok).
deň_v_týždni(sobota).
deň_v_týždni(nedeľa).

Riešenie 4-12:

študent(peter). % typ

dátum_narodenia(peter, 7-2-1980). % vlastnosť

miesto_narodenia(peter, bratislava). % vlastnosť

výška(peter, vysoký). % vlastnosť

vlastní(peter, bodrík). % vzťah

pes(bodrík). % typ

má_rád(peter, jana). % vzťah

študent(jana). % typ

žena(jana). % typ

muž(peter). % typ

Predikáty muž/1 a žena/1 sme použili na vyjadrenie rozdielu medzi študentom a študentkou.

Riešenie 4-13:

spoločný_nadriadený(Z1, Z2, NADRIADENÝ) :-
vedúci(NADRIADENÝ, Z1),
vedúci(NADRIADENÝ, Z2).

Riešenie 4-14:

pracovník(mrkvička, % meno
kivt, % katedra
asistent, % pracovné zaradenie
12, % odpracované roky
1000$). % plat
...

% katedra, kde pracuje pán Mrkvička?
?- pracovník(mrkvička, KATEDRA, _, _, _).

% vedúci katedry KIVT?
?- pracovník(VEDÚCI, kivt, vedúci, _, _).

% plat asistenta?
?- pracovník(_, _, asistent, _, PLAT).

Cieľ v bode c) sa splní opätovne toľkokrát, koľko asistentov je v databáze.

Riešenie 4-16:

JABLKO % premenná
struktura(a b c) % nič - chýbajú čiarky
slivka % atóm
osoba(peter) % štruktúra
2(X, Y) % nič - funktor 2 nie je atóm
'Bratislava % nič - chýba apostrof na konci
x_y_z % atóm
_xy_z % premenná
suma(s(0),s(S(0))) % nič - funktor S nie je atóm

Riešenie 5-1:

má_rád(emil, X) :- jedlo(X).
jedlo(jablko).
jedlo(kura).
jedlo(X) :- zjedol(Y,X), žije(Y).
zjedol(peter, banán).
žije(peter).

Reprezentácia faktov sa nemení, a preto ich neuvádzame.
" X [má_rád(emil, X) Ü jedlo(X )] " X [jedlo(X) Ü zjedol(Y, X) & žije(Y)]
" X [má_rád(emil, X) Ú Øjedlo(X)] " X [jedlo(X) Ú Øzjedol(Y, X) Ú Øžije(Y)]

Riešenie 5-2:

má_rád(juraj, X) :- jedlo(X), chuť(X, sladká). 
chuť(citrón, kyslá).
chuť(čokoláda, sladká).

jedlo(citrón).
jedlo(čokoláda).

" X [má_rád(juraj, X) Ü jedlo(X) & chuť(X, sladká)]
" X [má_rád(juraj, X) Ú Øjedlo(X) Ú Øchuť(X, sladká)]

Riešenie 5-4:

má_rád(emil, banán) Ú Øjedlo(banán)
jedlo(jablko)
jedlo(banán) Ú Øzjedol(peter, banán) Ú Øžije(peter)
zjedol(peter, banán)
žije(peter)
Ømá_rád(emil, banán) cieľ
Øjedlo(banán) (6. a 1.)
Øzjedol(peter, banán) Ú Øžije(peter) (7. a 3.)
Øžije(peter) (8. a 4.)
prázdna rezolventa (9. a 5.)

Riešenie 5-5:

c Ú Øa Ú Øb
a Ú Øb Ú Ød
b
d
c Ú Øb Ú Ød (1. a 2.)
c Ú Øa (1. a 3.)
a Ú Ød (2. a 3.)
a Ú Øb (2. a 4.)
c Ú Ød (5. a 3.)
c Ú Øb (5. a 4.)
a (7. a 4., 8. a 3.)
c (9. a 4., 10. a 3.)

Riešenie 5-6:

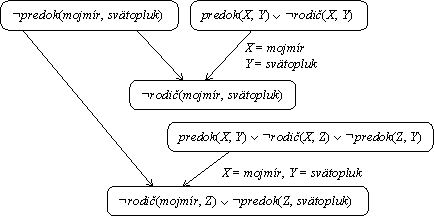
Ďalšie rezolventy sa nedajú odvodiť a teda hypotéza predok(mojmír, svätopluk) neplatí.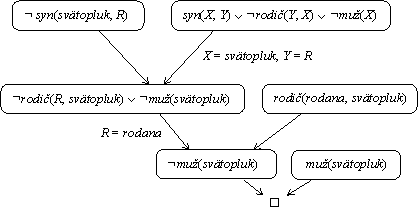

Riešenie 5-7:

?- čiara(bod(1,X), bod(2,Y)) = čiara(bod(X,1), bod(Y,2)).
X = 1
Y = 2 
yes

```
?- +(3, 2) = 5.
no
```
```
?- mínus(3, 2) = 1.
no
```
```
?- bod(1,2) = bod(1,2,X).
no
```

Riešenie 5-8:

vertikál(čiara(bod(X,_), bod(X,_)).
horizontál(čiara(bod(_,Y), bod(_,Y)).

Riešenie 5-9:

?- horizontál(čiara(bod(2,5), B).
B = bod(_002A, 5)
yes

?- horizontál(U), vertikál(U).
U = čiara(bod(_0025, _0026), bod(_0025, _0026)) 
yes

Riešenie 5-10:

stru(rodič(_,_)).

Riešenie 6-1:

Hlava Telo

jablko [hruška, slivka, banán]
jablko [hruška, [slivka], banán]
jablko [[hruška, slivka, banán]]
[jablko, hruška] [slivka, banán]
[jablko,hruška,slivka,banán] []

Riešenie 6-2:

```
[a, b, c, d]
[a, X]
```
Nepodobajú sa (prvý zoznam má päť prvkov a druhý dva).
```
[[a, b, c, d, e]]
[X | Y]
```
Podobajú sa: X = [a, b, c, d, e], Y = [].

Poznámka: Druhý zoznam sa podobá na ľubovoľný neprázdny zoznam.
```
[a, b, c, d, e]
[[X] | [b, c, d, e]]
```
Nepodobajú sa (prvý prvok prvého zoznamu je atóm a prvý prvok druhého zoznamu je jednoprvkový zoznam).
```
[a, b, c, d, e]
[a | [b, c, d, e]]
```
Podobajú sa.
```
[[a, b], [c, d], e]
[X | [Y | Z]]
```
Podobajú sa: X = [a, b], Y = [c, d], Z = [e].

[a, pred_b(X, [b,c]), c, pred_c([[3]]), d, e]
[X, pred_b(Y, Z), c, pred_c([P|Q]), d, e]

Podobajú sa: X = a, Y = X, Z = [b, c], P = [3], Q = [].

Riešenie 6-3:

zoznam([]).
zoznam([_|_]).

Takáto (často používaná) definícia predikátu zoznam/1 bez použitia rekurzie nezodpovedá zadaniu, lebo sa splní napr. pre argument [a|b], ktorý nie je zoznam. Často sa používa pre svoju jednoduchosť. Správna definícia predikátu zoznam/1 by mala byť takáto:

zoznam([]).
zoznam([_|T] :- zoznam(T).

Riešenie 6-4:

tri_prvky([_,_,_]).

Riešenie 6-5:

sublist(X, L) :-
spoj(L1, _, L), % L1 je prefix L taký, 
spoj(_, X, L1). % že X je sufix L1 
spoj([], L, L).
spoj([X|T1], L2, [X|T]) :- spoj(T1, L2, T).

?- sublist(X, [a,b]).
X = [] ->;
X = [a] ->;
X = [] ->;
X = [a, b] ->;
X = [b] ->;
X = [] ->;
no

Riešenie 6-6:

last([X], X).
last([_|T], X) :- last(T, X).

butlast([_], []).
butlast([X|T], [X|ShrtT]) :- butlast(T, ShrtT).

postfix([], X, [X]).
postfix([H|T], X, [H|LngT]) :- postfix(T, X, LngT).

S použitím predikátu spoj/3 (pozri riešenie cvičenia 6-5):

last2(L, X) :- spoj(_, [X], L).

butlast2(L, ShrtL) :- spoj(ShrtL, [_], L).

postfix2(L, X, LngL) :- spoj(L, [X], LngL).

Riešenie 6-7:

subset1([], L).
subset1([X|L1], L2) :-
member(X, L2), subset1(L1, L2).

member(X, [X | _]).
member(X, [_ | Tail]) :- member(X, Tail).

Predikát subset1/2 možno použiť na test vzťahu podmnožina medzi dvoma danými množinami. Ide o procedurálnu definíciu predikátu: daná množina Set1 je podmnožinou množiny Set2, ak sa všetky prvky množiny Set1 nachádzajú v množine Set2, t.j. na zistenie vzťahu podmnožina treba postupne prechádzať prvky množiny Set1 a použitím predikátu member/2 zisťovať, či sa nachádzajú v množine Set2.

Na generovanie všetkých podmnožín danej množiny definíciu predikátu subset1/2 nemožno použiť.

Iná definícia predikátu subset môže byť takáto:

% relácia podmnožina, v ktorej však
subset_aux([],[]). % záleží na poradí prvkov
subset_aux(S, [H|T]) :-
subset_aux(R,T), % existuje podmnožina R taká, že
( S = R % S je R
; % alebo
S = [H|R] ) % S je R spolu s hlavou druhého argumentu

set_equal(Set1, Set2) :- % rovnosť množín (nezáleží na poradí)
permutácia(Set1, Set2).

permutácia([],[]).
permutácia(L, [H|T]) :-
del(H,L,R),
permutácia(R,T).

del(X, [X|T], T).
del(X, [Y|T], [Y|T1]) :- del(X, T, T1).

subset2(Set1, Set2) :-
subset_aux(X, Set2),
set_equal(X, Set1).

Predikát subset2/2 možno použiť aj na generovanie všetkých podmnožín danej množiny. Vygenerujú sa však všetky permutácie, t.j. všetky zoznamy, ktorými možno reprezentovať podmnožinu danej množiny.

Dopyt subset2(X,[a,b,c]) bude mať 16 riešení (zoznamy [], [a], [b], [a,b], [b,a], [c], [a,c], [c,a], [b,c], [c,b], [a,b,c], [a,c,b], [b,a,c], [b,c,a], [c,a,b], [c,b,a]).

Na generovanie podmnožín možno použiť aj predikát subset_aux/2, ktorý vygeneruje pre každú podmnožinu iba jeden zoznam (prvky v poradí danej množiny - druhý argument). Dotaz subset_aux(X,[a,b,c]) bude mať iba 8 riešení (zoznamy [], [a], [b], [a,b], [c], [a,c], [b,c], [a,b,c]).

Riešenie 6-8:

del_all([], [], _).
del_all([H|T1], T2, H) :-
del_all(T1, T2, H).
del_all([H|T1], [H|T2], X) :-
del_all(T1, T2, X).

?- del_all([a,b,a,a], L, a).

L = [b] -> ;
L = [b,a] -> ;
L = [b,a] -> ;
L = [b,a,a] -> ;
L = [a,b] -> ;
L = [a,b,a] -> ;
L = [a,b,a] -> ;
L = [a,b,a,a] ->;
no

Ak chceme, aby alternatívne pokusy o splnenie cieľa del_all([a,b,a,a],L,a) boli neúspešné treba do poslednej klauzuly doplniť test, ktorým zabezpečíme, aby sa klauzuly navzájom vylučovali:

del_all([H|T1], [H|T2], X) :-
H \= X, 
del_all(T1, T2, X).

Riešenie 6-9:

preklad_chyby(1, integer_overflow).
preklad_chyby(2, division_by_zero).
preklad_chyby(3, unknown_identifier).

Vo všeobecnosti sa treba vyhýbať použitiu predikátu = vždy, keď možno použiť automatické zisťovanie podobnosti a naviazanie hodnôt na premenné.

Riešenie 6-10:

Predikát neznámy/2 zamení každý druhý prvok zoznamu (prvý argument) atómom tajné. Prvé a druhé pravidlo riešia prípad prázdneho, resp. jednoprvkového zoznamu. Tretie pravidlo hovorí, že ak máme zoznam s aspoň dvoma prvkami (X a Y), tak druhý z nich nahradíme atómom tajné po rekurzívnom spracovaní zvyšku zoznamu.

V definícii predikátu neznámy/2 treba na reprezentáciu ukončovacej podmienky dve klauzuly: jednu pre zoznamy s párnym počtom prvkov (prázdny zoznam) a druhú pre zoznamy s nepárnym počtom prvkov (jednoprvkový zoznam).

Riešenie 6-11:

párny([]).
párny([_,_|L]) :- párny(L).

Riešenie 6-12:

preklad([], []).
preklad([S_head | S_tail], [E_head | E_tail]) :-
slovník(S_head, E_head),
preklad(S_tail, E_tail).

slovník(jozef, joe).
slovník(pije, drinks).
slovník(mlieko, milk).

Riešenie 6-13:

porovnaj(List, Element) :-
spoj(T, [Element | T], List).

Generuje vo všeobecnom tvare, všetky zoznamy, kde druhý argument je "v strede":

?- porovnaj(L, a).
L = [a] ->;
L = [_1, a, _1] ->;
L = [_1, _2, a, _1, _2] ->;
...

Riešenie 6-14:

?- X = 2, Y is X + 1.
X = 2, Y = 3 ->
yes

?- X = 2, Y = X + 1.
X = 2, Y = 2 + 1 ->
yes

```
?- X = 2, Y == X + 1.
no
```
```
?- X = 2, Y =:= X + 1.
no
```
```
?- X = 2, 3 =:= X + 1.
yes
```

Riešenie 6-15:

```
?- 2 + 1 is 6 mod 4 + 1.
no
```
```
?- X = 5 + 2, Y = 8 - 1, X == Y.
no
```
```
?- Bohatý = Chudobný.
yes
```
```
?- Hlúpy \= Primitívny.
no
```
```
?- Hlúpy \== Primitívny.
yes
```

Riešenie 6-16:

sumy([], 0, 0).
sumy([H|T], Nova_kladná, Záporná) :-
H >= 0,
sumy(T, Kladná, Záporná),
Nová_kladná is Kladná + H.

sumy([H|T], Kladná, Nová_záporná) :-
H < 0,
sumy(T, Kladná, Záporná),
Nová_zaporná is Záporná + H.

Riešenie 6-17:

Pri definícii predikátu gcd vychádzame zo známych pravidiel pre výpočet najväčšieho spoločného deliteľa D dvoch čísel X a Y:

ak X a Y sú rovnaké, potom D = X;
ak X < Y, potom D sa rovná najväčšiemu spoločnému deliteľovi X a rozdielu Y-X;
ak Y < X, potom urob to isté ako v prípade 2) s vymenenými X a Y.

V prologu:

gcd(X, X, X).
gcd(X, Y, D) :-
X < Y,
Y1 is Y - X,
gcd(X, Y1, D).
gcd(X,Y,D) :-
Y < X,
gcd(Y, X, D).

Riešenie 6-18:

max([X], X).
max([X | T], Max) :-
max(T, Y),
( Y >= X, Max = Y
;
Y < X, Max = X
).

Riešenie 6-19:

faktoriál(0, 1).
faktoriál(N, F) :- faktoriál(N1, F1),
N is N1 + 1,
F is N * F1.

Takto definovaný predikát možno použiť aj na zistenie čísla zo známej hodnoty jeho faktoriálu:

?- faktoriál(N, 5040).
N = 7 ->
yes

Pri pokuse o alternatívne riešenie sa interpret prologu dostane do nekonečného cyklu.

Riešenie 6-20:

Takto upravený predikát druhá_mocnina/2 definuje reláciu medzi zoznamom termov a zoznamom, ktorý obsahuje všetky prvky prvého zoznamu transformované takto: ak ide o číslo transformuje sa na druhú mocninu, v prípade nečíselných termov sa tieto nemenia. Pridaná klauzula (druhá_mocnina(X, X).) rieši aj prípad prázdneho zoznamu (klauzula druhá_mocnina([], []).).

Odporúčame čitateľovi zistiť správanie pri hľadaní alternatívnych riešení.

Riešenie 6-21:

počítaj_kladné2([],0).
počítaj_kladné2([H|T], N) :-
number(H), H >= 0,
počítaj_kladné2(T, NT),
N is NT + 1.
počítaj_kladné2([H|T], N) :-
number(H), H < 0,
počítaj_kladné2(T, N).
počítaj_kladné2([H|T], N) :-
počítaj_kladné2(T, N).

Pridaním testu not(number(H)) do poslednej klauzuly zabezpečíme, aby pri spätnom chode prolog nenašiel alternatívne (a nesprávne) riešenie.

Riešenie 6-22:

počítaj_kladné3([H|T], N) :-
počítaj_kladné3(H, N1),
počítaj_kladné3(T, N2),
N is N1 + N2.
počítaj_kladné3(E, 1) :- number(E), E >= 0.
počítaj_kladné3(_, 0).

Riešenie 6-23:

párne([], []).
párne([H|T], [H|T1]) :-
0 is H mod 2,
párne(T, T1).
párne([H | T], T1) :-
1 is H mod 2,
párne(T, T1).

Riešenie 6-24:

počítaj_párne([], 0).
počítaj_párne([H|T], N) :-
0 is H mod 2,
počítaj_párne(T, M),
N is M + 1.
počítaj_párne([H|T], N) :-
1 is H mod 2,
počítaj_párne(T, N).

Riešenie 6-25:

hľadaj_párne(X, [X|_]) :- 0 is X mod 2.
hľadaj_párne(X, [_|T]) :- hľadaj_párne(X, T).

Riešenie 6-26:

redukuj_zoznamy([L], L).
redukuj_zoznamy([L|T], X) :-
redukuj_zoznamy(T, Y),
spoj(L, Y, X). % pozri riešenie cvičenia 6-5

V prípade, že prvý argument môže byť ľubovoľný nelineárny zoznam, t.j. jeho prvkami môžu byť ďalšie zoznamy zoznamov, treba použiť viacnásobnú rekurziu:

redukuj_zoznamy2([L], L).
redukuj_zoznamy2([L|T], X) :-
redukuj_zoznamy2(L, LY),
redukuj_zoznamy2(T, TY),
spoj(LY, TY, X).
redukuj_zoznamy2(X, [X]).

Riešenie 6-27:

pridaj(X, L, L) :- member(X, L), !.
pridaj(X, L, [X | L]).

Takto definovaný predikát pridaj/3 pracuje podľa očakávania iba v prípade, ak sú prvé dva argumenty vstupné a posledný výstupný (t.j. voľná premenná). Predikát sa teda nedá použiť na testovanie definovanej relácie, lebo v niektorých prípadoch sa úspešne splní napriek tomu, že relácia podľa špecifikácie neplatí:

?- pridaj(2, [2], [2, 2]).
yes

Uvedený nedostatok vyriešime porovnaním druhého a tretieho argumentu v prvej klauzule až po splnení predikátu rez (pozri aj poznámku v kapitole 6, str. *):

pridaj(X, L1, L2) :- member(X, L), !, L1 = L2.
pridaj(X, L, [X | L]).

Riešenie 6-28:

```
?- p(X).
X = 1 ->;
X = 2 ->;
no
```

?- p(X), p(Y).
X = 1, Y = 1 ->;
X = 1, Y = 2 ->;
X = 2, Y = 1 ->;
X = 2, Y = 2 ->;
no

?- p(X), !, p(Y).
X = 1, Y = 1 ->;
X = 1, Y = 2 ->;
no

Riešenie 6-30:

```
?- známka(90, 'Nedostatočne').
yes
```
Chybný predikát známka/2 možno použiť iba na určenie známky na základe daného počtu bodov (druhý argument premenná). Aby sme mohli predikát použiť aj ako test, treba porovnanie argumentov umiestniť až za rez (pozri aj riešenia cvičenia 6-27):
```
známka(Body, Z) :- Body >= 92, !, Z = 'Výborne'.
známka(Body, Z) :- Body >= 76, !, Z = 'Veľmi dobre'.
známka(Body, Z) :- Body >= 62, !, Z = 'Dobre'.
známka(Body, 'Nedostatočne').
```

Riešenie 6-31:

not_equal(X, Y) :- X == Y, !, fail.
not_equal(_, _).

Riešenie 6-32:

?- member(X, Platné), not(member(X, Neplatné)).

Riešenie 6-33:

d_member(X, [H | _]) :- d_member(X, H).
d_member(X, [_ | T]) :- d_member(X, T).
d_member(X, X) :- not(list(X)).

list([]).
list([_|T]) :- list(T).

Podmienka not(list(X)) v poslednej klauzule predikátu d_member/2 je dôležitá preto, aby pri spätnom chode v prípade generovania prvkov zoznamu (prvý argument výstupný a druhý vstupný) prolog nenašiel nesprávne alternatívne odpovede.

Riešenie 6-34:

vypíš_zoznam([]).
vypíš_zoznam([H|T]) :-
write(H),
vypíš_zoznam(T).

vypíš_zoznam([]).
vypíš_zoznam([H|T]) :-
vypíš_zoznam(T),
write(H).

Poradie klauzúl v oboch prípadoch možno zameniť bez zmeny deklaratívnej sémantiky.

Riešenie 6-35:

:- op(800, xf, kg).
:- op(850, yfx, plus).
:- op(800, fx, gram).
:- op(900, xfx, sa_rovná).
:- op(800, xf, libra).

sa_rovná(plus(kg(1.2), gram(500)), libra(X))

Riešenie 6-36:

+++(<<-(a, b), c)
+++(<<-(a,b), ->>(c,d))
<->(a, ->>(---(b,c), d))
<<-(a, ->>(b, c))
<<-(a, ->>(->>(b, c), d))
operátor <-> je definovaný ako neasociatívny, a preto tento zápis sa nepovoľuje
->>(->>(a, b), c)
<->(<<-(a, b), ->>(c, d))
<<-(a, ->>(---(b, c), d))

Riešenie 6-37:

:- op(600, fx, pán).
:- op(600, fx, pánovi).
:- op(600, fx, pani).
:- op(650, xfx, je_vedúci).
:- op(650, xfx, je_vedúca).

Riešenie 6-38:

zobraz_súbor(Súbor) :-
see(Súbor),
sprac_obsahu(0),
seen.

sprac_obsahu(N) :- % N značí aktuálne číslo riadka
read(Term),
výpis_termu(Term, N),
N1 is N + 1, 
sprac_obsahu(N1).
sprac_obsahu(_).

výpis_termu(end_of_file, _) :- !, fail.
výpis_termu(Term, N) :-
write(N), tab(1), write(Term), nl.

Všimnite si modifikáciu schémy spracovania súboru pomocou rekurzie, ktorú sme uviedli v učebnici.

Riešenie 6-39:

vytvor_študent(VstS, VystS, Študent) :-

see(VstS), tell(VystS),

repeat,

read(Term),

( Term = end_of_file, !,

seen, told

;

Term = študent(_,Študent, _,_),

write(Term), 
write('.'), nl, % ukončenie termu

fail ).

Riešenie 6-40:

nájdi(Súbor, Term) :-
see(Súbor),
read(NTerm),
spracuj_súbor(Term, NTerm),
seen.

spracuj_súbor(_, end_of_file) :- !. % koniec
spracuj_súbor(Term, NTerm) :-
výpis(Term, NTerm),
read(Dalsi),
spracuj_súbor(Term, Dalsi).

výpis(Term, Term) :- !, write(Term), nl. % podobaju sa
výpis(_, _). % inak

Riešenie 6-41:

mocnina :- 
write('Zadajte číslo: '),
read(X),
spracuj(X).

spracuj(stop) :- !.
spracuj(N) :- 
mocnina(N, C),
write('Druhá mocnina čísla '), 
write(N),
write(' je '), 
write(C), nl,
mocnina.
spracuj(_) :- mocnina. % zadané iné ako číslo alebo atóm stop

mocnina(N, C) :- 
number(N), 
C is N * N.

mocnina2 :-
repeat,
write('Zadajte číslo: '),
read(N),
( N = stop, !
;
mocnina(N, C),
write('Druhá mocnina čísla '), 
write(N),
write(' je '), 
write(C), nl,
fail ).
mocnina2.

Riešenie 6-42:

ulož_študent(Súbor, Študent) :-
see(Súbor),
read(Term),
spracuj_študent(Term, Študent),
seen.

spracuj_študent(end_of_file, _) :- !.
spracuj_študent(študent(I, S, P, Z), S) :-
!, assertz(študent(I, S, P, Z)),
read(Nový),
spracuj_študent(Nový, S).
spracuj_študent(_, S) :-
read(Nový),
spracuj_študent(Nový, S).

ulož_študent2(Súbor, Študent) :-
see(Súbor),
repeat,
read(Term),
( Term = end_of_file, !,
seen
;
Term = študent(_, Študent, _, _),
assertz(Term),
fail ).

Riešenie 6-43:

ulož_študent3(Súbor, Študent) :-

see(Súbor),

repeat,

read(Term),

( Term = end_of_file, !,

seen

;

Term = študent(_, Študent, _, _),

not(Term),

assertz(Term),

fail ).

Riešenie 6-44:

študent_štrukt_do_zoznamu(VstS, VystS) :-

see(VstS), tell(VystS),

repeat,

read(Term),

( Term = end_of_file, !,

seen, told

;

Term = študent(I, S, P, Z),

write([I, S, P, Z]),
write('.'), nl, 

fail ).

Do súboru sa zoznamy ukladajú ukončené bodkou a novým riadkom, aby sa dali jednoducho neskôr načítať použitím predikátu read.

Riešenie 6-45:

setq(Symbol, Value, Evaluated_Value) :-
atom(Symbol),
eval(Value, Evaluated_Value),
SymbolV =.. [Symbol, Evaluated_Value],
assertz(SymbolV).

set(Symbol, Evaluated_Value, Evaluated_Value) :-
atom(Symbol),
SymbolV =.. [Symbol, Evaluated_Value],
assertz(SymbolV).

defun(Fun_Name, Args, Form, Fun_Name) :-
append(Args, [Value], ArgV),
Head =.. [Fun_Name| ArgV],
assertz((Head :- eval(Form, Value))).

Riešenie 6-46:

študent_zoznam do_štrukt(VstS, VystS) :-

see(VstS), tell(VystS),

repeat,

read(Term),

( Term = end_of_file, !,

seen, told

;

Štrukt =.. [študent|Term],

write(VystH, Štrukt),

fail ).

Riešenie 6-47:

vytvor_študent :-
načítaj('Identifikačné číslo: ', I, interval(I,1,1000)),
načítaj('Meno: ', M, atom(M)),
načítaj('Predmet: ', P, atom(P)),
načítaj('Známka: ', Z,
member(Z,[výborne,veľmi_dobre,dobre,nedostatočne])),
assertz(študent(I, M, P, Z)),
ďalej('áno/nie?:', vytvor_študent). % pokračovať?

vytvor_študent.

načítaj(Text, Term, Test) :-
write(Text), read(Term),
call(Test), !. % správny vstup
načítaj(Text, Term, Ohraničenie) :- % znovu
načítaj(Text, Term, Ohraničenie).

interval(I, From, To) :- 
I >= From, I =< To.

ďalej(Text, Cieľ) :- % splní sa iba pri načítaní termu ano
write(Text),
read(ano),
call(Cieľ).

to Homepage to Books to the Top

Last updated:
Mária Bieliková bielik [zavináč] fiit-dot-stuba-dot-sk